Untuk mempelajari materi Program Linear, sebaiknya adik-adik harus mempelajari terlebih dahulu materi tentang sistem pertidaksamaan linear dua variabel. Dengan mempelajari sistem pertidaksamaan linear dua variabel, adik-adik paham tentang Daerah Himpunan Penyelesaian (DHP) Sistem Pertidaksamaan linear Dua variabel. Untuk mempelajarinya adik-adik bisa klik tautan berikut:
Sistem Pertidaksamaan Linear Dua Variabel. Diharapkan adik-adik benar-benar mempelajarinya karena sistem Pertidaksamaan linear Dua Variabel merupakan dasar untuk memahami Program Linear Dengan Metode Uji Titik Pojok. Pelajari juga tentang Menentukan Nilai Optimum dengan Metode Garis selidik. Menentukan nilai optimum dengan metode uji titik pojok, mengharuskan kita untuk mencari titik-titik pojok dari daerah penyelesaian kendala atau syarat-syarat kemudian mensubstitusikan kedalam fungsi objektif. Saat ini admin menganggap bahwa adik-adik sudah mempelajarinya dan sudah paham segala teknik menggambar garis dan menentukan arah arsiran. Kalau begitu kita mulai dengan soal-soal dan pembahasannya.
Berdasarkan daya tampung:
x + y ≤ 40
Berdasarkan harga beli dan modal:
12.000x + 10.000y ≤ 450.000 disederhanakan menjadi,
6x + 5y ≤ 225
Jeruk harus ada, maka x ≥ 0
Jambu harus ada, maka y ≥ 0
Dengan demikian model matematika yang sesuai adalah:
x + y ≤ 40; 6x + 5y ≤ 225; x ≥ 0; y ≥ 0
Jawab: B.
Fungsi objekti atau fungsi sasaran:
z = 5000x + 4000y
Kertas:
2x + 2y ≤ 50, disederhanakan menjadi x + y ≤ 25
Titik potong sumbu x = (25, 0)
Titik potong sumbu y = (0, 25)
a = 1 > 0 dan tanda pertidaksamaan ≤, maka arsiran
ke arah kiri garis.
Pita:
2x + y ≤ 40
Titik potong sumbu x = (20, 0)
Titik potong sumbu y = (0, 40)
a = 2 > 0 dan tanda pertidaksamaan ≤ maka arsiran
ke arah kiri garis.
x ≥ 0
Arsiran ke arah kanan sumbu y.
y ≥ 0
Arsiran ke arah atas sumbu x.
Jawab: C.
Fungsi sasaran atau fungsi objektif:
f(x, y) = z = 150000x + 100000y
Kain polos:
x + 2y ≤ 20
Titik potong sumbu x = (20, 0)
titik potong sumbu y = (0, 10)
a = 1 > 0 dan tanda pertidaksamaan ≤, maka arsiran
ke arah kiri garis.
Kain bergaris:
3x + y ≤ 20
Titik potong sumbu x = (20/3, 0)
Titik potong sumbu y = (0, 20)
a = 3 > 0 dan tanda pertidaksamaan ≤, maka arsiran
ke arah kiri garis.
x ≥ 0
Arsiran ke arah kanan sumbu y.
y ≥ 0
Arsiran ke arah atas sumbu x.
Jawab: A.
Fungsi objektif:
z = 50000x + 60000y
Kain katun:
x + 2,5y ≤ 70
Titik potong sumbu x = (70, 0)
Titik potong sumbu y = (0, 28)
a = 1 > 0 dan tanda pertidaksamaan ≤ maka arsiran
ke arah kiri garis.
Kain sutera:
2x + 1,5y ≤ 84
Titik potong sumbu x = (42, 0)
Titik potong sumbu y = (0, 56)
a = 2 > 0 dan tanda pertidaksamaan ≤, maka arsiran
ke arah kiri garis.
x ≥ 0
Arsiran ke arah kanan sumbu y.
y ≥ 0
Arsiran ke arah atas sumbu x.
dan y(jenis B) = 16 buah.
Jawab: E.
Jumlah kandang maksimum 8:
x + y ≤ 8
Jumlah ternak maksimum 100:
15x + 6y ≤ 100
Harus ada kambing:
x ≥ 0
Harus ada sapi:
y ≥ 0
jadi model matematika yang tepat adalah:
15x + 6y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
Jawab: B.
Tepung:
3x + 2y ≤ 5
Gula:
x + 2y ≤ 3
Margarin:
0,5x + 0,5y ≤ 1
Kue bika harus ada:
x ≥ 0
Kue putri salju harus ada:
y ≥ 0
jadi model matematika yang tepat adalah:
x + 2y ≤ 3; 3x + 2y ≤ 5; 0,5x + 0,5y ≤ 1; x ≥ 0; y ≥ 0
Jawab: A.
Fungsi objektif:
f(x, y) = z = 30000x + 50000y
Soda:
2x + 2y ≤ 40 disederhanakan menjadi x + y ≤ 20
Titik potong sumbu x = (20, 0)
Titik potong sumbu y = (0, 20)
Arsiran ke arah kiri garis.
Susu:
x + 3y ≤ 30
Titik potong sumbu x = (30, 0)
Titik potong sumbu y = (0, 10)
Arsiran ke arah kiri garis.
x ≥ 0
Arsiran ke arah kanan sumbu y.
y ≥ 0
Arsiran ke arah atas sumbu x.
Jawab: D.
Titik A adalah titik potong antara garis x = 1 dan y = 2, dengan demikian koordinat titik A(1, 2). Titik B adalah titik potong antara garis y = 2 dengan garis x + y = 6. Masukkan y = 2 kedalam persamaan x + y = 6.
x + 2 = 6
x = 4
Dengan demikian koordinat titik B(4, 2)
Titik C(3, 3)
Titik D adalah titik potong garis x = 1 dengan 2x + 3y = 15.
2.1 + 3y = 15
3y = 13
y = 13/3
Dengan demikian koordinat titik D(1, 13/3)
Jawab: A.
Misalkan banyak beras campuran pertama = x dan banyak beras campuran kedua = y.
Tinjau beras jenis A !
$4x + 8y \leq 80$ → disederhanakan menjadi:
$x + 2y \leq 20$
Tinjau beras jenis B !
$8x + 10y \leq 106$ → disederhanakan menjadi:
$4x + 5y \leq 53$
$x \geq 0$
$y \geq 0$
Cari titik potong garis $x + 2y = 20$ dengan garis $4x + 5y = 53$
$4x + 8y = 80$
$4x + 5y = 53$
------------------------ --
$3y = 27$
$y = 9\ ton = 9000\ kg$
$x = 2\ ton = 2000\ kg$
Penjualan maksimum $= Rp840.000.000,00$
jawab: C.
Misalkan jumlah rumah tipe I = x unit dan jumlah rumah tipe II = y unit.
Jumlah rumah:
$x + y \leq 125$
Luas lahan:
$100x + 75y \leq 10.000$ → disederhanakan menjadi:
$4x + 3y = 400$
Fungsi objektif $f(x, y) = 250.000.000x + 200.000.000y$
Perhatikan gambar !
Substitusikan titik-titik kritis (titik-titik pojok) ke dalam persamaan fungsi objektif $f(x, y) = 250.000.000x + 200.000.000y$.
Terlihat bahwa penghasilan maksimum adalah Rp26.250.000.000,00.
jawab: B.
$x + y ≤ 3$
$3x + 2y ≥ 6$
$y ≥ 0$
Daerah penyelesaian adalah daerah yang diarsir.
$L = \dfrac{1}{2}.1.3$
$L = \dfrac{3}{2}$
jawab: D.
Demikianlah soal dan pembahasan program linear uji titik pojok. Selamat belajar !
SHARE THIS POST
Artikel Terkait:
1. Menentukan Nilai Optimum Dengan Metode Garis Selidik
2. Menentukan Daerah Himpunan Penyelesaian Sistem Pertidaksamaan Linier Dua Variabel
www.maretong.com
Sistem Pertidaksamaan Linear Dua Variabel. Diharapkan adik-adik benar-benar mempelajarinya karena sistem Pertidaksamaan linear Dua Variabel merupakan dasar untuk memahami Program Linear Dengan Metode Uji Titik Pojok. Pelajari juga tentang Menentukan Nilai Optimum dengan Metode Garis selidik. Menentukan nilai optimum dengan metode uji titik pojok, mengharuskan kita untuk mencari titik-titik pojok dari daerah penyelesaian kendala atau syarat-syarat kemudian mensubstitusikan kedalam fungsi objektif. Saat ini admin menganggap bahwa adik-adik sudah mempelajarinya dan sudah paham segala teknik menggambar garis dan menentukan arah arsiran. Kalau begitu kita mulai dengan soal-soal dan pembahasannya.
Soal dan Pembahasan Program Linear
1. Nilai minimum dari $f(x, y) = 3x + 2y$ yang memenuhi daerah penyelesaian sistem pertidaksamaan $4x + 5y \leq 20$; $3x + 5y \geq 15$; $x \geq 0$; $y \geq 0$ adalah . . . .
A. 6
B. 8
C. 10
D. 12
E. 15
[Soal UN Matematika IPS 2016]
A. 6
B. 8
C. 10
D. 12
E. 15
[Soal UN Matematika IPS 2016]
$\bullet$ $4x + 5y \leq 20$
Titik potong sumbu x = (5, 0)
Titik potong sumbu y = (0, 4)
a = 4 > 0 dan tanda pertidaksamaan $\leq$, maka arsiran
ke arah kiri garis.
$\bullet$ $3x + 5y \geq 15$
Titik potong sumbu x = (5, 0)
Titik potong sumbu y = (0, 3)
a = 3 > 0 dan tanda pertidaksamaan $\geq$, maka arsiran
ke arah kanan garis.
$\bullet$ $x \geq 0$
Arsiran ke arah kanan sumbu y.
$\bullet$ $y \geq 0$
Arsiran ke arah atas sumbu x.
Perhatikan gambar !
Jawab: A.
Titik potong sumbu x = (5, 0)
Titik potong sumbu y = (0, 4)
a = 4 > 0 dan tanda pertidaksamaan $\leq$, maka arsiran
ke arah kiri garis.
$\bullet$ $3x + 5y \geq 15$
Titik potong sumbu x = (5, 0)
Titik potong sumbu y = (0, 3)
a = 3 > 0 dan tanda pertidaksamaan $\geq$, maka arsiran
ke arah kanan garis.
$\bullet$ $x \geq 0$
Arsiran ke arah kanan sumbu y.
$\bullet$ $y \geq 0$
Arsiran ke arah atas sumbu x.
Perhatikan gambar !
-----------------------------
Fungsi sasaran
f(x, y) = z = 3x + 2y
-----------------------------
Titik pojok Nilai z
-----------------------------
A(5, 0) z = 3.5 + 2.0 = 15
B(0, 4) z = 3.0 + 2.4 = 8
C(0, 3) z = 3.0 + 2.3 = 6
-----------------------------
Jadi nilai minimum z = 6 pada titik pojok C(0, 3)Jawab: A.
2. Seorang pedagang buah mempunyai tempat yang hanya dapat menampung 40 kg buah-buahan. Jeruk dibeli dengan harga Rp12.000,00 per kg dan jambu dibeli dengan harga Rp10.000,00 per kg. Pedagang tersebut mempunyai modal Rp450.000,00 untuk membeli $x$ kg jeruk dan $y$ kg jambu. Model Matematika yang sesuai dengan masalah tersebut adalah . . . .
A. x + y ≤ 40; 6x + 5y ≤ 450; x ≥ 0; y ≥ 0
B. x + y ≤ 40; 6x + 5y ≤ 225; x ≥ 0; y ≥ 0
C. x + y ≥ 40; 6x + 5y ≤ 450; x ≥ 0; y ≥ 0
D. x + y ≥ 40; 6x + 5y ≤ 225; x ≥ 0; y ≥ 0
E. x + y ≥ 40; 6x + 5y ≥ 225; x ≥ 0; y ≥ 0
[Soal UN Matematika IPS 2016]
A. x + y ≤ 40; 6x + 5y ≤ 450; x ≥ 0; y ≥ 0
B. x + y ≤ 40; 6x + 5y ≤ 225; x ≥ 0; y ≥ 0
C. x + y ≥ 40; 6x + 5y ≤ 450; x ≥ 0; y ≥ 0
D. x + y ≥ 40; 6x + 5y ≤ 225; x ≥ 0; y ≥ 0
E. x + y ≥ 40; 6x + 5y ≥ 225; x ≥ 0; y ≥ 0
[Soal UN Matematika IPS 2016]
Berdasarkan daya tampung:
x + y ≤ 40
Berdasarkan harga beli dan modal:
12.000x + 10.000y ≤ 450.000 disederhanakan menjadi,
6x + 5y ≤ 225
Jeruk harus ada, maka x ≥ 0
Jambu harus ada, maka y ≥ 0
Dengan demikian model matematika yang sesuai adalah:
x + y ≤ 40; 6x + 5y ≤ 225; x ≥ 0; y ≥ 0
Jawab: B.
3. Pada sebuah supermarket, seorang karyawati menyediakan jasa pembungkus kado. untuk membungkus kado jenis A dibutuhkan 2 lembar kertas pembungkus dan 2 meter pita. Sedangkan untuk membungkus kado jenis B dibutuhkan 2 lembar kertas pembungkus dan 1 meter pita. Tersedia kertas pembungkus 50 lembar dan pita 40 meter. Upah untuk membungkus setiap kado jenis A dan untuk membungkus setiap kado jenis B berturut-turut adalah Rp.5000,00 dan Rp4.000,00. Upah maksimum yang dapat diterima oleh karyawati tersebut adalah . . . .
A. Rp75.000,00
B. Rp100.000,00
C. Rp115.000,00
D. Rp125.000,00
E. Rp160.000,00
[Soal UN Matematika IPS 2016]
A. Rp75.000,00
B. Rp100.000,00
C. Rp115.000,00
D. Rp125.000,00
E. Rp160.000,00
[Soal UN Matematika IPS 2016]
Fungsi objekti atau fungsi sasaran:
z = 5000x + 4000y
Kertas:
2x + 2y ≤ 50, disederhanakan menjadi x + y ≤ 25
Titik potong sumbu x = (25, 0)
Titik potong sumbu y = (0, 25)
a = 1 > 0 dan tanda pertidaksamaan ≤, maka arsiran
ke arah kiri garis.
Pita:
2x + y ≤ 40
Titik potong sumbu x = (20, 0)
Titik potong sumbu y = (0, 40)
a = 2 > 0 dan tanda pertidaksamaan ≤ maka arsiran
ke arah kiri garis.
x ≥ 0
Arsiran ke arah kanan sumbu y.
y ≥ 0
Arsiran ke arah atas sumbu x.
----------------------------
Fungsi Sasaran
f(x, y) = z = 5000x + 4000y
----------------------------
Titik pojok Nilai z
----------------------------
A(0, 0) z = 0
B(20, 0) z = 100000
C(15, 10) z = 115000
D(0, 25) z = 100000
----------------------------
Upah maksimum = Rp115.000,00Jawab: C.
4. Seorang penjahit memiliki persediaan 20 m kain polos dan 20 m kain bergaris untuk membuat 2 jenis pakaian. Pakaian model I memerlukan 1 m kain polos dan 3 m kain bergaris. Pakaian model II memerlukan 2 m kain polos dan 1 m kain bergaris. Pakaian model I dijual dengan harga Rp150.000,00 per potong, dan pakaian model II dijual dengan harga Rp100,000,00 per potong. Penghasilan maksimum yang dapat diperoleh penjahit tersebut adalah . . . .
A. Rp1.400.000,00
B. Rp1.600.000,00
C. Rp1.800.000,00
D. Rp1.900.000,00
E. Rp2.000.000,00
[Soal UN Matematika IPA 2016]
A. Rp1.400.000,00
B. Rp1.600.000,00
C. Rp1.800.000,00
D. Rp1.900.000,00
E. Rp2.000.000,00
[Soal UN Matematika IPA 2016]
Fungsi sasaran atau fungsi objektif:
f(x, y) = z = 150000x + 100000y
Kain polos:
x + 2y ≤ 20
Titik potong sumbu x = (20, 0)
titik potong sumbu y = (0, 10)
a = 1 > 0 dan tanda pertidaksamaan ≤, maka arsiran
ke arah kiri garis.
Kain bergaris:
3x + y ≤ 20
Titik potong sumbu x = (20/3, 0)
Titik potong sumbu y = (0, 20)
a = 3 > 0 dan tanda pertidaksamaan ≤, maka arsiran
ke arah kiri garis.
x ≥ 0
Arsiran ke arah kanan sumbu y.
y ≥ 0
Arsiran ke arah atas sumbu x.
--------------------------------
Fungsi Sasaran
f(x, y) = z = 150000x + 110000y
--------------------------------
Titik pojok Nilai z
--------------------------------
A(0, 0) z = 0
B(20/3, 0) z = 1000000
C(4, 8) z = 1400000
D(0, 10) z = 1000000
--------------------------------
Penghasilan maksimum = Rp1.400.000,00Jawab: A.
5. Seorang penjahit membuat dua jenis pakaian. Pakaian jenis A memerlukan kain katun 1 m dan kain sutera 2 m, sedangkan pakaian jenis B memerlukan kain katun 2,5 m dan kain sutera 1,5 m. Bahan katun yang tersedia 70 m dan kain sutera 84 m. Pakaian jenis A dijual dengan laba Rp50.000,00/buah, sedangkan pakaian jenis B dijual dengan laba Rp60.000,00/ buah. Agar penjahit memperoleh laba maksimum, banyak pakaian jenis A dan jenis B yang terjual berturut-turut adalah . . . .
A. 20 dan 16
B. 26 dan 20
C. 30 dan 6
D. 16 dan 30
E. 30 dan 16
[Soal UN Matematika IPA 2017]
A. 20 dan 16
B. 26 dan 20
C. 30 dan 6
D. 16 dan 30
E. 30 dan 16
[Soal UN Matematika IPA 2017]
Fungsi objektif:
z = 50000x + 60000y
Kain katun:
x + 2,5y ≤ 70
Titik potong sumbu x = (70, 0)
Titik potong sumbu y = (0, 28)
a = 1 > 0 dan tanda pertidaksamaan ≤ maka arsiran
ke arah kiri garis.
Kain sutera:
2x + 1,5y ≤ 84
Titik potong sumbu x = (42, 0)
Titik potong sumbu y = (0, 56)
a = 2 > 0 dan tanda pertidaksamaan ≤, maka arsiran
ke arah kiri garis.
x ≥ 0
Arsiran ke arah kanan sumbu y.
y ≥ 0
Arsiran ke arah atas sumbu x.
------------------------------
Fungsi Sasaran
f(x, y) = z = 50000x + 60000y
------------------------------
Titik pojok Nilai z
------------------------------
A(42, 0) z = 2100000
B(30, 16) z = 2460000
C(0, 28) z = 1680000
D(0, 0) z = 0
------------------------------
Laba maksimum = Rp2.400.000,00 dengan x (jenis A) = 30 buahdan y(jenis B) = 16 buah.
Jawab: E.
6. Seorang peternak memiliki tidak lebih dari 8 kandang untuk memelihara kambing dan sapi. Setiap kandang dapat menampung kambing sebanyak 15 ekor atau menampung sapi sebanyak 6 ekor. Jumlah ternak yang direncanakan tidak lebih dari 100 ekor. Jika banyak kandang yang terisi kambing x buah dan yang terisi sapi y buah, model matematika untuk kegiatan peternak tersebut adalah . . . .
A. 8x + 6y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
B. 15x + 6y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
C. 6x + 15y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
D. 6x + 8y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
E. 15x + 8y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
[Soal UN Matematika IPS 2017]
A. 8x + 6y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
B. 15x + 6y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
C. 6x + 15y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
D. 6x + 8y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
E. 15x + 8y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
[Soal UN Matematika IPS 2017]
Jumlah kandang maksimum 8:
x + y ≤ 8
Jumlah ternak maksimum 100:
15x + 6y ≤ 100
Harus ada kambing:
x ≥ 0
Harus ada sapi:
y ≥ 0
jadi model matematika yang tepat adalah:
15x + 6y ≤ 100, x + y ≤ 8, x ≥ 0, y ≥ 0
Jawab: B.
7. Diketahui sistem pertidaksamaan 2x + 3y ≥ 9, x + y ≥ 4, x ≥ 0, y ≥ 0. Nilai minimum z = 4x + 3y untuk x dan y pada daerah penyelesaian sistem pertidaksamaan tersebut adalah . . . .
A. 18
B. 16
C. 15
D. 13
E. 12
[Soal UN Matematika IPS 2017]
A. 18
B. 16
C. 15
D. 13
E. 12
[Soal UN Matematika IPS 2017]
Kita bisa juga membuat titik potong sumbu x dan y dalam bentuk
tabel seperti berikut:
Jawab: E.
tabel seperti berikut:
--------------------------------
Fungsi Sasaran
f(x, y) = z = 4x + 3y
--------------------------------
Titik pojok Nilai z
--------------------------------
A(9/2, 0) z = 4.9/2 + 3.0 = 18
B(3, 1) z = 4.3 + 3.1 = 15
C(0, 4) z = 4.0 + 3.4 = 12
--------------------------------
Nilai minimum = 12.Jawab: E.
8. Seorang wiraswasta kue basah memiliki bahan baku 5 kg tepung, 3 kg gula, dan 1 kg margarin. Untuk membuat kue bika memerlukan 3 kg tepung, 1 kg gula, dan 0,5 kg margarin. Sedangkan untuk kue putri salju memerlukan 2 kg tepung, 2 kg gula, dan 0,5 kg margarin. Jika x menyatakan banyak kue bika dan y menyatakan banyak kue putri salju, model matematika dari masalah tersebut adalah . . . .
A. x + 2y ≤ 3; 3x + 2y ≤ 5; 0,5x + 0,5y ≤ 1; x ≥ 0; y ≥ 0
B. x + 2y ≥ 3; 3x + 2y ≥ 5; 0,5x + 0,5y ≤ 1; x ≥ 0; y ≥ 0
C. x + 2y ≤ 3; 3x + 2y ≥ 5; 0,5x + 0,5y ≥ 1; x ≥ 0; y ≥ 0
D. x + 2y ≥ 3; 3x + 2y ≤ 5; 0,5x + 0,5y ≥ 1; x ≥ 0; y ≥ 0
E. x + 2y ≤ 3; 3x + 2y ≤ 5; 0,5x + 0,5y ≥ 1; x ≥ 0; y ≥ 0
[Soal UN matematika IPS 2018]
A. x + 2y ≤ 3; 3x + 2y ≤ 5; 0,5x + 0,5y ≤ 1; x ≥ 0; y ≥ 0
B. x + 2y ≥ 3; 3x + 2y ≥ 5; 0,5x + 0,5y ≤ 1; x ≥ 0; y ≥ 0
C. x + 2y ≤ 3; 3x + 2y ≥ 5; 0,5x + 0,5y ≥ 1; x ≥ 0; y ≥ 0
D. x + 2y ≥ 3; 3x + 2y ≤ 5; 0,5x + 0,5y ≥ 1; x ≥ 0; y ≥ 0
E. x + 2y ≤ 3; 3x + 2y ≤ 5; 0,5x + 0,5y ≥ 1; x ≥ 0; y ≥ 0
[Soal UN matematika IPS 2018]
Tepung:
3x + 2y ≤ 5
Gula:
x + 2y ≤ 3
Margarin:
0,5x + 0,5y ≤ 1
Kue bika harus ada:
x ≥ 0
Kue putri salju harus ada:
y ≥ 0
jadi model matematika yang tepat adalah:
x + 2y ≤ 3; 3x + 2y ≤ 5; 0,5x + 0,5y ≤ 1; x ≥ 0; y ≥ 0
Jawab: A.
9. Untuk membuat 1 liter minuman jenis A diperlukan 2 kaleng soda dan 1 kaleng susu, sedangkan untuk membuat 1 liter minuman jenis B diperlukan 2 kaleng soda dan 3 kaleng susu. Tersedia 40 kaleng soda dan 30 kaleng susu. Jika 1 liter minuman jenis A dijual seharga Rp30.000,00 dan 1 liter minuman jenis B dijual seharga Rp50.000,00, pendapatan maksimum dari hasil penjualan kedua jenis minuman tersebut adalah . . . .
A. Rp500.000,00
B. Rp540.000,00
C. Rp600.000,00
D. Rp700.000,00
E. Rp720.000,00
[Soal UN Matematika IPA 2018]
A. Rp500.000,00
B. Rp540.000,00
C. Rp600.000,00
D. Rp700.000,00
E. Rp720.000,00
[Soal UN Matematika IPA 2018]
Fungsi objektif:
f(x, y) = z = 30000x + 50000y
Soda:
2x + 2y ≤ 40 disederhanakan menjadi x + y ≤ 20
Titik potong sumbu x = (20, 0)
Titik potong sumbu y = (0, 20)
Arsiran ke arah kiri garis.
Susu:
x + 3y ≤ 30
Titik potong sumbu x = (30, 0)
Titik potong sumbu y = (0, 10)
Arsiran ke arah kiri garis.
x ≥ 0
Arsiran ke arah kanan sumbu y.
y ≥ 0
Arsiran ke arah atas sumbu x.
------------------------------
Fungsi Sasaran
f(x, y) = z = 30000x + 50000y
------------------------------
Titik pojok Nilai z
------------------------------
A(20, 0) z = 600000
B(15, 5) z = 700000
C(0, 10) z = 500000
D(0, 0) z = 0
------------------------------
Pendapatan maksimum = Rp700.000,00Jawab: D.
10. Nilai maksimum dari $f(x, y) = 2x + 3y$ pada daerah yang dibatasi oleh: $(3x + y - 9)(2x + y - 8) \leq 0$, $x \geq 0$, $y \geq 0$ sama dengan . . . .
A. 6
B. 8
C. 20
D. 24
E. 27
[Soal SBMPTN]
A. 6
B. 8
C. 20
D. 24
E. 27
[Soal SBMPTN]
$(3x + y - 9)(2x + y - 8) \leq 0\ (negatif)\ artinya:$
$A.\ 3x + y - 9 \geq 0\ (+)$ dan $2x + y - 8 \leq 0\ (-)$
atau
$B.\ 3x + y - 9 \leq 0\ (-)$ dan $2x + y - 8 \geq 0\ (+)$
Kerjakan satu per satu !
A. $3x + y - 9 \geq 0\ (+)$ dan $2x + y - 8 \leq 0\ (-)$
1. $3x + y - 9 \geq 0$
$3x + y \geq 9$
Titik potong sumbu x = (3, 0)
Titik potong sumbu y = (0, 9)
Arah arsiran ke arah kanan garis.
2. $2x + y - 8 \leq 0$
$2x + y \leq 8$
Titik potong sumbu x = (4, 0)
Titik potong sumbu y = (0, 8)
Arah arsiran ke arah kiri garis.
Daerah penyelesaian A adalah $1 ∩ 2$.
B. $3x + y - 9 \leq 0\ (-)$ dan $2x + y - 8 \geq 0\ (+)$
1. $3x + y \leq 9$
Titik potong sumbu x = (3, 0)
Titik potong sumbu y = (0, 9)
Arah arsiran ke arah kiri garis.
2. $2x + y - 8 \geq 0$
$2x + y \geq 8$
Titik potong sumbu x = (4, 0)
Titik potong sumbu y = (0, 8)
Arah arsiran ke arah kanan garis.
Daerah penyelesaian B adalah $1 ∩ 2$.
Ada dua daerah penyelesaian yaitu daerah penyelesaian A dan daerah penyelesaian B. Daerah penyelesaian akhir adalah gabungan dari penyelesaian A dan B.
Jawab: E.
$A.\ 3x + y - 9 \geq 0\ (+)$ dan $2x + y - 8 \leq 0\ (-)$
atau
$B.\ 3x + y - 9 \leq 0\ (-)$ dan $2x + y - 8 \geq 0\ (+)$
Kerjakan satu per satu !
A. $3x + y - 9 \geq 0\ (+)$ dan $2x + y - 8 \leq 0\ (-)$
1. $3x + y - 9 \geq 0$
$3x + y \geq 9$
Titik potong sumbu x = (3, 0)
Titik potong sumbu y = (0, 9)
Arah arsiran ke arah kanan garis.
2. $2x + y - 8 \leq 0$
$2x + y \leq 8$
Titik potong sumbu x = (4, 0)
Titik potong sumbu y = (0, 8)
Arah arsiran ke arah kiri garis.
Daerah penyelesaian A adalah $1 ∩ 2$.
B. $3x + y - 9 \leq 0\ (-)$ dan $2x + y - 8 \geq 0\ (+)$
1. $3x + y \leq 9$
Titik potong sumbu x = (3, 0)
Titik potong sumbu y = (0, 9)
Arah arsiran ke arah kiri garis.
2. $2x + y - 8 \geq 0$
$2x + y \geq 8$
Titik potong sumbu x = (4, 0)
Titik potong sumbu y = (0, 8)
Arah arsiran ke arah kanan garis.
Daerah penyelesaian B adalah $1 ∩ 2$.
Ada dua daerah penyelesaian yaitu daerah penyelesaian A dan daerah penyelesaian B. Daerah penyelesaian akhir adalah gabungan dari penyelesaian A dan B.
---------------------------------
Fungsi Sasaran
f(x, y) = z = 2x + 3y
---------------------------------
Titik pojok Nilai z
---------------------------------
A(3, 0) z = 2.3 + 3.0 = 6
B(4, 0) z = 2.4 + 3.0 = 8
C(1, 6) z = 2.1 + 3.6 = 20
D(0, 8) z = 2.0 + 3.8 = 24
E(0, 9) z = 2.0 + 3.9 = 27
----------------------------------
Nilai maksimum = 27.Jawab: E.
11. Agar fungsi $f(x, y) = ax + 10y$ dengan kendala $2x + y ≥ 12$, $x + y ≥ 10$, $x ≥ 0$, $y ≥ 0$ mencapai minimum hanya di $(2, 8)$, maka konstanta $a$ memenuhi . . . .
$A.\ -20 \leq a \leq -10$
$B.\ 10 \leq a \leq 20$
$C.\ 10 \leq a \leq 20$
$D.\ 10 < a \leq 20$
$E.\ 10 < a < 20$
[Soal SPMB 2004]
$A.\ -20 \leq a \leq -10$
$B.\ 10 \leq a \leq 20$
$C.\ 10 \leq a \leq 20$
$D.\ 10 < a \leq 20$
$E.\ 10 < a < 20$
[Soal SPMB 2004]
$\bullet$ $2x + y ≥ 12$
Titik potong sumbu x = (6, 0)
Titik potong sumbu y = (0, 12)
Arsiran ke arah kanan garis.
$\bullet$ $x + y \geq 10$
Titik potong sumbu x = (10, 0)
Titik potong sumbu y = (0, 10)
Arsiran ke arah kanan garis
$2a + 80$, akibatnya:
$2a + 80 \leq 10a$
$80 \leq 10a - 2a$
$80 \leq 8a$
$10 \leq a$
$a \geq 10$ . . . . *
$2a + 80 \leq 120$
$2a \leq 40$
$a \leq 20$ . . . . **
$dari\ *\ dan\ **$
$10 \leq a \leq 20$
Jawab: B.
Titik potong sumbu x = (6, 0)
Titik potong sumbu y = (0, 12)
Arsiran ke arah kanan garis.
$\bullet$ $x + y \geq 10$
Titik potong sumbu x = (10, 0)
Titik potong sumbu y = (0, 10)
Arsiran ke arah kanan garis
----------------------------------- Fungsi Sasaran f(x, y) = z = ax + 10y ----------------------------------- Titik pojok Nilai z ----------------------------------- A(10, 0) z = a.10 + 0 = 10a B(2, 8) z = a.2 + 10.8 = 2a + 80 C(0, 12) z = a.0 + 10.12 = 120 -----------------------------------Karena titik $B(2, 8)$ adalah titik minimum, maka nilai minimum adalah
$2a + 80$, akibatnya:
$2a + 80 \leq 10a$
$80 \leq 10a - 2a$
$80 \leq 8a$
$10 \leq a$
$a \geq 10$ . . . . *
$2a + 80 \leq 120$
$2a \leq 40$
$a \leq 20$ . . . . **
$dari\ *\ dan\ **$
$10 \leq a \leq 20$
Jawab: B.
12. Dalam himpunan penyelesaian pertidaksamaan $x \geq 1$, $y \geq 2$, $x + y \leq 6$, $2x + 3y \leq 15$, maka nilai minimum dari $3x + 4y$ sama dengan . . . .
A. 9
B. 10
C. 11
D. 12
E. 13
[Soal UMPTN '98]
A. 9
B. 10
C. 11
D. 12
E. 13
[Soal UMPTN '98]
Titik A adalah titik potong antara garis x = 1 dan y = 2, dengan demikian koordinat titik A(1, 2). Titik B adalah titik potong antara garis y = 2 dengan garis x + y = 6. Masukkan y = 2 kedalam persamaan x + y = 6.
x + 2 = 6
x = 4
Dengan demikian koordinat titik B(4, 2)
Titik C(3, 3)
Titik D adalah titik potong garis x = 1 dengan 2x + 3y = 15.
2.1 + 3y = 15
3y = 13
y = 13/3
Dengan demikian koordinat titik D(1, 13/3)
-----------------------
Fungsi Sasaran
f(x, y) = z = 3x + 4y
-----------------------
Titik pojok Nilai z
-----------------------
A(1, 2) z = 11
B(4, 2) z = 20
C(3, 3) z = 21
D(1, 13/3) z = 20,33
-----------------------
Nilai minimum = 11.Jawab: A.
13. Himpunan penyelesaian sistem pertidaksamaan $2y - x \leq 2$, $4x + 3y \leq 12$, $x \geq 0$, $y \geq 0$ pada gambar di bawah adalah . . . .
$A.\ I$
$B.\ II$
$C.\ III$
$D.\ I\ dan\ IV$
$E.\ II\ dan\ III$
[Soal UN Matematika IPS '99]
$A.\ I$
$B.\ II$
$C.\ III$
$D.\ I\ dan\ IV$
$E.\ II\ dan\ III$
[Soal UN Matematika IPS '99]
$2y - x \leq 2$
Titik potong sumbu $x = (-2, 0)$
Titik potong sumbu $y = (0, 1)$
Menentukan arah arsiran:
cara 1.
$a = -1 \leq 0$ dan tanda pertidaksamaan $\leq$, maka
arah arsiran adalah ke arah kanan garis.
cara 2.
$b = 2 \geq 0$ dan tanda pertidaksamaan adalah $\leq$, maka
arah arsiran adalah ke arah bawah garis.
$4x + 3y \leq 12$
Titik potong sumbu $x = (3, 0)$
Titik potong sumbu $y = (0, 4)$
Menentukan arah arsiran:
$a = 4 \geq 0$ dan tanda pertidaksamaan $\leq$, maka
arah arsiran adalah ke arah kiri garis.
Dengan demikian, himpunan penyelesaian adalah daerah $I$.
Jawab: A.
Titik potong sumbu $x = (-2, 0)$
Titik potong sumbu $y = (0, 1)$
Menentukan arah arsiran:
cara 1.
$a = -1 \leq 0$ dan tanda pertidaksamaan $\leq$, maka
arah arsiran adalah ke arah kanan garis.
cara 2.
$b = 2 \geq 0$ dan tanda pertidaksamaan adalah $\leq$, maka
arah arsiran adalah ke arah bawah garis.
$4x + 3y \leq 12$
Titik potong sumbu $x = (3, 0)$
Titik potong sumbu $y = (0, 4)$
Menentukan arah arsiran:
$a = 4 \geq 0$ dan tanda pertidaksamaan $\leq$, maka
arah arsiran adalah ke arah kiri garis.
Dengan demikian, himpunan penyelesaian adalah daerah $I$.
Jawab: A.
14. Nilai maksimum dari 5x + 4y pada daerah himpunan penyelesaian berikut adalah . . . .
A. 8
B. 11
C. 12
D. 14
E. 15
A. 8
B. 11
C. 12
D. 14
E. 15
Persamaan garis yang melalui titik $(0, a)$ dan $(b, 0)$
adalah $ax + by = ab$.
Persamaan garis yang melalui titik $(0, 2)$ dan $(4, 0)$
adalah $2x + 4y = 8$ disederhanakan menjadi $x + 2y = 4$.
Persamaan garis yang melalui titik $(0, 3)$ dan $(2, 0)$
adalah $3x + 2y = 6$.
Eliminasi kedua garis:
$3x + 2y = 6$
$x + 2y = 4$
------------------------ -
$2x = 2$
$x = 1$
$y = \dfrac32$
Titik-titik ekstrim dari daerah himpunan penyelesaian:
(0, 2), (0, 3), dan (1, 3/2).
Jawab: C.
adalah $ax + by = ab$.
Persamaan garis yang melalui titik $(0, 2)$ dan $(4, 0)$
adalah $2x + 4y = 8$ disederhanakan menjadi $x + 2y = 4$.
Persamaan garis yang melalui titik $(0, 3)$ dan $(2, 0)$
adalah $3x + 2y = 6$.
Eliminasi kedua garis:
$3x + 2y = 6$
$x + 2y = 4$
------------------------ -
$2x = 2$
$x = 1$
$y = \dfrac32$
Titik-titik ekstrim dari daerah himpunan penyelesaian:
(0, 2), (0, 3), dan (1, 3/2).
-------------------------------- Fungsi Sasaran f(x, y) = z = 5x + 4y -------------------------------- Titik pojok Nilai z -------------------------------- (0, 2) z = 5.0 + 4.2 = 8 (0, 3) z = 5.0 + 4.3 = 12 (1, 3/2) z = 5.1 + 4.3/2 = 11 --------------------------------Nilai maksimum = 12.
Jawab: C.
15. Setiap hari seorang pengrajin tas memproduksi dua jenis tas. Modal untuk tas model $I$ adalah Rp20.000,00 dengan keuntungan 40%. Modal untuk tas model $II$ adalah Rp30.000,00 dengan keuntungan 30%. Jika modal yang tersedia setiap harinya adalah Rp1.000.000,00 dan paling banyak hanya dapat memproduksi 40 tas, keuntungan terbesar yang dapat dicapai pengrajin tas tersebut adalah . . . .
A. 30%
B. 34%
C. 36%
D. 38%
E. 40%
[Soal UN Matematika IPA 2017]
A. 30%
B. 34%
C. 36%
D. 38%
E. 40%
[Soal UN Matematika IPA 2017]
Keuntungan tas model $I$ = 40%.Rp20.000,00 = Rp8.000,00
Keuntungan tas model $II$ = 30%.Rp30.000,00 = Rp6.000,00
Fungsi objektif:
F(x, y) = z = 8000x + 9000y
Daya tampung:
x + y ≤ 40
Modal:
20000x + 30000y ≤ 1000000, disederhanakan menjadi:
2x + 3y = 100
x ≥ 0
y ≥ 0
Keuntungan maksimum = Rp340.000
$= \dfrac{Rp340.000}{Rp1.000.000}$
$= \dfrac{34}{100}$
$= 34$%
Jawab: B.
Keuntungan tas model $II$ = 30%.Rp30.000,00 = Rp6.000,00
Fungsi objektif:
F(x, y) = z = 8000x + 9000y
Daya tampung:
x + y ≤ 40
Modal:
20000x + 30000y ≤ 1000000, disederhanakan menjadi:
2x + 3y = 100
x ≥ 0
y ≥ 0
----------------------------
Fungsi Sasaran
f(x, y) = z = 8000x + 9000y
----------------------------
Titik pojok Nilai z
----------------------------
A(40, 0) z = 320000
B(20, 20) z = 340000
C(0, 100/3) z = 300000
----------------------------
Keuntungan maksimum = Rp340.000
$= \dfrac{Rp340.000}{Rp1.000.000}$
$= \dfrac{34}{100}$
$= 34$%
Jawab: B.
16. Daerah yang memenuhi sistem pertidaksamaan linear $3x + 4y \leq 96$; $x + y \leq 30$; $x \geq 0$; $y \geq 0$ adalah . . . .
$A.\ I$
$B.\ II$
$C.\ III$
$D.\ IV$
$E.\ V$
[UN 2019 Mtk IPA]
$A.\ I$
$B.\ II$
$C.\ III$
$D.\ IV$
$E.\ V$
[UN 2019 Mtk IPA]
$3x + 4y \leq 96$ → lakukan uji titik $O(0, 0)\ !$
$3.0 + 4.0 \leq 96$
$0 \leq 96$ → benar, berarti arsiran ke arah $O(0, 0)$
$x + y \leq 30$
$0 + 0 \leq 30$
$0 \leq 30$ → benar, berarti arsiran ke arah $O(0, 0)$.
$x \geq 0\ dan\ y \geq 0$ → kuadran I.
Dengan demikian, daerah di kuadran I yang dua kali arsir adalah daerah IV.
jawab: D.
$3.0 + 4.0 \leq 96$
$0 \leq 96$ → benar, berarti arsiran ke arah $O(0, 0)$
$x + y \leq 30$
$0 + 0 \leq 30$
$0 \leq 30$ → benar, berarti arsiran ke arah $O(0, 0)$.
$x \geq 0\ dan\ y \geq 0$ → kuadran I.
Dengan demikian, daerah di kuadran I yang dua kali arsir adalah daerah IV.
jawab: D.
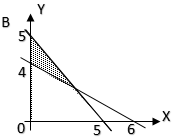
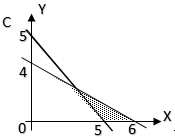
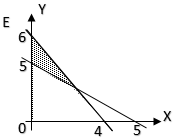
17. Daerah yang diarsir pada gambar di bawah ini adalah daerah penyelesaian dari pertidaksamaan . . . .
$A.\ 6x + y \leq 12;\ 5x + 4y \geq 20;\ x \geq 0;\ y \geq 0$
$B.\ 6x + y \geq 12;\ 5x + 4y \geq 20;\ x \geq 0;\ y \geq 0$
$C.\ 6x + y \geq 12;\ 5x + 4y \leq 20;\ x \geq 0;\ y \geq 0$
$D.\ x + 6y \leq 12;\ 4x + 5y \geq 20;\ x \geq 0;\ y \geq 0$
$E.\ x + 6y \geq 12;\ 4x + 5y \leq 20;\ x \geq 0;\ y \geq 0$
[UN 2019 Mtk IPA]
$A.\ 6x + y \leq 12;\ 5x + 4y \geq 20;\ x \geq 0;\ y \geq 0$
$B.\ 6x + y \geq 12;\ 5x + 4y \geq 20;\ x \geq 0;\ y \geq 0$
$C.\ 6x + y \geq 12;\ 5x + 4y \leq 20;\ x \geq 0;\ y \geq 0$
$D.\ x + 6y \leq 12;\ 4x + 5y \geq 20;\ x \geq 0;\ y \geq 0$
$E.\ x + 6y \geq 12;\ 4x + 5y \leq 20;\ x \geq 0;\ y \geq 0$
[UN 2019 Mtk IPA]
Ingat persamaan garis yang melalui titik $(0, a)\ dan\ (b, 0)$ adalah $ax + by = ab$
Perhatikan garis yang melalui titik $(4, 0)\ dan\ (0, 5)\ !$
$5x + 4y = 20$
$a = 5 > 0$ dan arsiran di sebelah kanan garis, berarti tanda pertidaksamaan adalah $\geq$. Pertidaksamaannya menjadi $5x + 4y \geq 20$.
Perhatikan garis yang melalui titik $(2, 0)\ dan\ (0, 12)\ !$
$12x + 2y = 24$ → disederhanakan menjadi:
$6x + y = 12$
$a = 6 > 0$ dan arsiran di sebelah kiri garis, berarti tanda pertidaksamaan adalah $\leq$. Pertidaksamaannya menjadi $6x + y \leq 12$.
Karena arsiran berada di kuadran I, maka: $x \geq 0\ dan\ y \geq 0$.
jawab: A.
Perhatikan garis yang melalui titik $(4, 0)\ dan\ (0, 5)\ !$
$5x + 4y = 20$
$a = 5 > 0$ dan arsiran di sebelah kanan garis, berarti tanda pertidaksamaan adalah $\geq$. Pertidaksamaannya menjadi $5x + 4y \geq 20$.
Perhatikan garis yang melalui titik $(2, 0)\ dan\ (0, 12)\ !$
$12x + 2y = 24$ → disederhanakan menjadi:
$6x + y = 12$
$a = 6 > 0$ dan arsiran di sebelah kiri garis, berarti tanda pertidaksamaan adalah $\leq$. Pertidaksamaannya menjadi $6x + y \leq 12$.
Karena arsiran berada di kuadran I, maka: $x \geq 0\ dan\ y \geq 0$.
jawab: A.
18. Seorang pedagang beras akan membuat beras campuran dengan cara mencampur beras jenis A dan beras jenis B. Beras campuran pertama terdiri dari 4 kg beras jenis A dan 8 kg beras jenis B sedangkan beras campuran kedua terdiri dari 8 kg beras jenis A dan 10 kg beras jenis B. Beras yang tersedia untuk beras jenis A dan B berturut-turut 80 ton dan 106 ton. Jika harga jual untuk beras campuran jenis pertama Rp60.000,00 dan jenis kedua Rp80.000,00, penjualan mksimum yang diperoleh adalah . . . .
$A.\ Rp1.200.000.000,00$
$B.\ Rp920.000.000,00$
$C.\ Rp840.000.000,00$
$D.\ Rp800.000.000,00$
$E.\ Rp795.000.000,00$
[UN 2019 Mtk IPA]
$A.\ Rp1.200.000.000,00$
$B.\ Rp920.000.000,00$
$C.\ Rp840.000.000,00$
$D.\ Rp800.000.000,00$
$E.\ Rp795.000.000,00$
[UN 2019 Mtk IPA]
| Campuran I (x) | Campuran II (y) | Tersedia | |
| Jenis A | 4 kg | 8 kg | 80 kg |
| Jenis B | 8 kg | 10 kg | 106 kg |
Misalkan banyak beras campuran pertama = x dan banyak beras campuran kedua = y.
Tinjau beras jenis A !
$4x + 8y \leq 80$ → disederhanakan menjadi:
$x + 2y \leq 20$
Tinjau beras jenis B !
$8x + 10y \leq 106$ → disederhanakan menjadi:
$4x + 5y \leq 53$
$x \geq 0$
$y \geq 0$
Cari titik potong garis $x + 2y = 20$ dengan garis $4x + 5y = 53$
$4x + 8y = 80$
$4x + 5y = 53$
------------------------ --
$3y = 27$
$y = 9\ ton = 9000\ kg$
$x = 2\ ton = 2000\ kg$
| $f(x,\ y) = 60.000x + 80.000y$ | |
| A(13.250, 0) | 795.000.000 |
| B(2.000, 9.000) | 840.000.000 |
| C(0, 10.000) | 800.000.000 | D(0, 0) | 0 |
Penjualan maksimum $= Rp840.000.000,00$
jawab: C.
19. Daerah yang diarsir pada grafik berikut adalah himpunan penyelesaian sistem pertidaksamaan linear. Nilai maksimum dari fungsi objektif $f(x, y) = 6x + 10y$ adalah . . . .
$A.\ 46$
$B.\ 40$
$C.\ 34$
$D.\ 30$
$E.\ 24$
[UN 2019 Mtk IPS]
$A.\ 46$
$B.\ 40$
$C.\ 34$
$D.\ 30$
$E.\ 24$
[UN 2019 Mtk IPS]
Koordinat titik kritis yang belum didapat adalah titik potong garis lurus. Untuk itu kita cari terlebih dahulu persamaan kedua garis, kemudian lakukan eliminasi.
Ingat !
Persamaan garis yang melalui titik $(0, a)\ dan\ (b, 0)$ adalah $ax + by = ab$
Garis yang melalui titik $(0, 2)\ dan\ (-1, 0)$
$2x - y = -2$ . . . . *
Garis yang melalui titik $(0, 5)\ dan\ (5, 0)$
$5x + 5y = 25$ → disederhanakan menjadi:
$x + y = 5$ . . . . **
Eliminasi persamaan * dan **
$2x - y = -2$
$x + y = 5$
-------------------- +
$3x = 3$
$x = 1$
$1 + y = 5$
$y = 4$
Uji titik-titik kritis (titik-titik pojok) ke dalam fungsi objektif $f(x, y) = 6x + 10y\ !$
$(0, 0) → 0$
$(5, 0) → 6.5 + 10.0 = 30$
$(0, 2) → 6.0 + 10.2 = 20$
$(1, 4) → 6.1 + 10.4 = 46$
Terlihat bahwa nilai maksimumnya adalah 46.
jawab: A.
Ingat !
Persamaan garis yang melalui titik $(0, a)\ dan\ (b, 0)$ adalah $ax + by = ab$
Garis yang melalui titik $(0, 2)\ dan\ (-1, 0)$
$2x - y = -2$ . . . . *
Garis yang melalui titik $(0, 5)\ dan\ (5, 0)$
$5x + 5y = 25$ → disederhanakan menjadi:
$x + y = 5$ . . . . **
Eliminasi persamaan * dan **
$2x - y = -2$
$x + y = 5$
-------------------- +
$3x = 3$
$x = 1$
$1 + y = 5$
$y = 4$
Uji titik-titik kritis (titik-titik pojok) ke dalam fungsi objektif $f(x, y) = 6x + 10y\ !$
$(0, 0) → 0$
$(5, 0) → 6.5 + 10.0 = 30$
$(0, 2) → 6.0 + 10.2 = 20$
$(1, 4) → 6.1 + 10.4 = 46$
Terlihat bahwa nilai maksimumnya adalah 46.
jawab: A.
20. Seorang pengusaha perumahan mempunyai lahan tanah seluas 10.000 $m^2$ yang akan dibangun rumah tipe I dan tipe II. Rumah tipe I memerlukan tanah seluas 100 $m^2$ dan rumah tipe II memerlukan tanah seluas 75 $m^2$. Jumlah rumah yang dibangun paling banyak 125 unit. Rumah tipe I dijual dengan Rp250.000.000,00 per unit dan rumah tipe II dijual dengan harga Rp200.000.000,00 per unit. Penghasilan maksimum yang dapat diperoleh pengusaha perumahan tersebut adalah . . . .
$A.\ Rp25.000.000.000,00$
$B.\ Rp26.250.000.000,00$
$C.\ Rp26.600.000.000,00$
$D.\ Rp26.670.000.000,00$
$E.\ Rp31.250.000.000,00$
[UN 2019 Mtk IPS]
$A.\ Rp25.000.000.000,00$
$B.\ Rp26.250.000.000,00$
$C.\ Rp26.600.000.000,00$
$D.\ Rp26.670.000.000,00$
$E.\ Rp31.250.000.000,00$
[UN 2019 Mtk IPS]
| Type I (x) | Type II (y) | Tersedia | |
| Luas lahan | 100 $m^2$ | 75 $m^2$ | 10.000 $m^2$ |
| Jumlah rumah | 1 | 1 | 125 unit |
Misalkan jumlah rumah tipe I = x unit dan jumlah rumah tipe II = y unit.
Jumlah rumah:
$x + y \leq 125$
Luas lahan:
$100x + 75y \leq 10.000$ → disederhanakan menjadi:
$4x + 3y = 400$
Fungsi objektif $f(x, y) = 250.000.000x + 200.000.000y$
Perhatikan gambar !
Substitusikan titik-titik kritis (titik-titik pojok) ke dalam persamaan fungsi objektif $f(x, y) = 250.000.000x + 200.000.000y$.
| f(x, y) = 250.000.000x + 200.000.000y | |
| A(0, 0) | 0 |
| B(100, 0) | Rp25.000.000.000,00 |
| C(25, 100) | Rp26.250.000.000,00 | D(0, 125) | Rp25.000.000.000,00 |
Terlihat bahwa penghasilan maksimum adalah Rp26.250.000.000,00.
jawab: B.
21. Grafik berikut yang merupakan penyelesaian sistem pertidaksamaan linier
$\begin{cases} 3x + 2y \geqslant 12\\ x + y \leq 5 \\ y\geq 0 \\ x\geqslant 0\end{cases}$ adalah . . . .
[UN 2018 Mtk IPS]
$\begin{cases} 3x + 2y \geqslant 12\\ x + y \leq 5 \\ y\geq 0 \\ x\geqslant 0\end{cases}$ adalah . . . .
$(1).\ 3x + 2y ≥ 12$
Titik potong sumbu $X$ → $y = 0 → (4, 0)$
Titik potong sumbu $Y$ → $x = 0 → (0, 6)$
uji titik $(0, 0)$ → $3.0 + 2.0 = 0 < 12$, arsiran menjauhi titik $(0, 0)$
karena yang diminta adalah $≥ 12$
$(2).\ x + y ≤ 5$
Titik potong sumbu $X$ → $y = 0$ → $(5, 0)$
Titik potong sumbu $y$ → $x = 0$ → $(0, 5)$
Uji titik $(0, 0)$ → $0 + 0 = 0 < 5$, arsiran menuju titik $(0, 0)$
karena yang diminta adalah $≤ 5$
(3) $x ≥ 0$ dan $y ≥ 0$ → kuadran I.
Jawab D.
Titik potong sumbu $X$ → $y = 0 → (4, 0)$
Titik potong sumbu $Y$ → $x = 0 → (0, 6)$
uji titik $(0, 0)$ → $3.0 + 2.0 = 0 < 12$, arsiran menjauhi titik $(0, 0)$
karena yang diminta adalah $≥ 12$
$(2).\ x + y ≤ 5$
Titik potong sumbu $X$ → $y = 0$ → $(5, 0)$
Titik potong sumbu $y$ → $x = 0$ → $(0, 5)$
Uji titik $(0, 0)$ → $0 + 0 = 0 < 5$, arsiran menuju titik $(0, 0)$
karena yang diminta adalah $≤ 5$
(3) $x ≥ 0$ dan $y ≥ 0$ → kuadran I.
Jawab D.
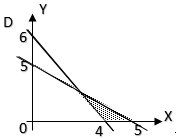
22. Daerah yang diarsir pada gambar di bawah adalah daerah himpunan penyelesaian semua (x, y) yang memenuhi sistem pertidaksamaan . . . .
A. x + y ≤ 4, 2x + 5y ≥ 10, y ≥ 0
B. x + y ≤ 4, 2x + 5y ≤ 10, y ≥ 0
C. x + y ≤ 4, 2x + 5y ≥ 10, x ≥ 0
D. x + y ≥ 4, 2x + 5y ≥ 10, x ≥ 0
A. x + y ≥ 4, 2x + 5y ≤ 10, x ≥ 0
[UN 2018 Mtk IPA]
A. x + y ≤ 4, 2x + 5y ≥ 10, y ≥ 0
B. x + y ≤ 4, 2x + 5y ≤ 10, y ≥ 0
C. x + y ≤ 4, 2x + 5y ≥ 10, x ≥ 0
D. x + y ≥ 4, 2x + 5y ≥ 10, x ≥ 0
A. x + y ≥ 4, 2x + 5y ≤ 10, x ≥ 0
[UN 2018 Mtk IPA]
Persamaan garis yang melalui titik (0, p) dan (q, 0)
$px + qy = pq$
Garis melalui titik (0, 4) dan (4, 0)
$4x + 4y = 16$
$x + y = 4$
Karena $a > 0$ dan arsiran ke arah kiri garis maka:
$x + y ≤ 4$
Garis melalui titik (0, 2) dan (5, 0)
$2x + 5y = 10$
Karena $a > 0$ dan arsiran ke arah kanan garis, maka:
$2x + 5y \geq 10$
Karena himpunan penyelesaian berada di kuadran I,
maka:
$x ≥ 0$
$y ≥ 0$
Jawab: C.
$px + qy = pq$
Garis melalui titik (0, 4) dan (4, 0)
$4x + 4y = 16$
$x + y = 4$
Karena $a > 0$ dan arsiran ke arah kiri garis maka:
$x + y ≤ 4$
Garis melalui titik (0, 2) dan (5, 0)
$2x + 5y = 10$
Karena $a > 0$ dan arsiran ke arah kanan garis, maka:
$2x + 5y \geq 10$
Karena himpunan penyelesaian berada di kuadran I,
maka:
$x ≥ 0$
$y ≥ 0$
Jawab: C.
23. Luas daerah penyelesaian sistem pertidaksamaan $x + y ≤ 3$, $3x + 2y ≥ 6$, $y ≥ 0$ adalah . . . . satuan luas.
$(A)\ \dfrac12$
$(B)\ \dfrac34$
$(C)\ \dfrac13$
$(D)\ \dfrac32$
$(E)\ 2$
[SBMPTN 2017 MDas]
$(A)\ \dfrac12$
$(B)\ \dfrac34$
$(C)\ \dfrac13$
$(D)\ \dfrac32$
$(E)\ 2$
[SBMPTN 2017 MDas]
$x + y ≤ 3$
$3x + 2y ≥ 6$
$y ≥ 0$
Daerah penyelesaian adalah daerah yang diarsir.
$L = \dfrac{1}{2}.1.3$
$L = \dfrac{3}{2}$
jawab: D.
Demikianlah soal dan pembahasan program linear uji titik pojok. Selamat belajar !
Artikel Terkait:
1. Menentukan Nilai Optimum Dengan Metode Garis Selidik
2. Menentukan Daerah Himpunan Penyelesaian Sistem Pertidaksamaan Linier Dua Variabel
www.maretong.com
Post a Comment for "Soal dan Pembahasan Program Linear Uji Titik Pojok"
Jika ada saran dan kritik yang sifatnya membangun atau ada koreksi silahkan tuliskan di kolom komentar.