Daftar isi
Pengertian Sudut Pusat dan Sudut keliling Lingkaran
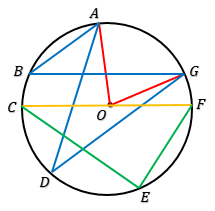
Pengertian, rumus dan cara menghitung Sudut Pusat dan Sudut Keliling lingkaran serta Contoh Soal dan Pembahasan Super Lengkap. Sudut pusat adalah sudut yang dibentuk oleh titik pusat dengan dua titik yang terletak pada lingkaran, sedangkan sudut keliling adalah sudut yang dibentuk oleh tiga titik yang terletak pada lingkaran. Perhatikan gambar!$\angle AOG,\ \angle AOF,\ \angle AOC,\ \angle COG,\ \angle FOG$ adalah contoh sudut pusat.
$\angle ABG,\ \angle ADG,\ \angle CEF,\ \angle FCE,\ \angle BGD$ adalah contoh sudut keliling.
Rumus Sudut Pusat dan Sudut Keliling Lingkaran
Jika sudut pusat dan sudut keliling menghadap busur yang sama, maka berlaku:$Sudut\ pusat = 2 \times sudut\ keliling$ atau $Sudut\ keliling = \dfrac12 \times sudut\ pusat$
$\angle AOG = 2 \times \angle ABG$ → sama-sama menghadap busur AG.
$\angle AOG = 2 \times \angle ADG$ → sama-sama menghadap busur AG.
Sifat-sifat:
1. Semua sudut keliling yang menghadap busur yang sama memiliki besar sudut yang sama.
$\angle ABG = \angle ADG = \dfrac12 \times \angle AOG$ → sama-sama menghadap busur AG atau $\widehat{AG}$.
2. Sudut keliling yang menghadap diameter besarnya $90^o$.
Garis CF merupakan diameter lingkaran, sedangkan sudut CEF menghadap garis CF sehingga $\angle CEF = 90^o$.
Untuk memperjelas pengertian sudut pusat dan sudut keliling, pelajari contoh soal dan pembahasan sudut pusat dan sudut keliling berikut berikut.
Contoh Soal dan Pembahasan Sudut Pusat dan Sudut Keliling Lingkaran
Soal nomor 1:Perhatikan gambar di bawah!
Diketahui O adalah titik pusat lingkaran. Besar sudut AOB adalah . . . .
$A.\ 15^o$
$B.\ 30^o$
$C.\ 45^o$
$D.\ 60^o$
[Sudut Pusat dan Sudut Keliling]
Pembahasan:
Sudut ACB adalah sudut keliling, sedangkan sudut AOB adalah sudut pusat. Sudut ACB dan sudut AOB sama-sama menghadap busur yang sama, yaitu busur AB. Dengan demikian besar sudut AOB sama dengan dua kali besar sudut ACB.
$\begin{align}
\angle AOB &= 2 \times \angle ACD\\
&= 2 \times 30^o\\
&= 60^o\\
\end{align}$
jawab: D.
Soal nomor 2:
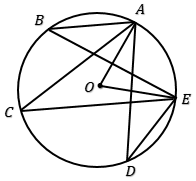
Perhatikan gambar!
Titik O adalah titik pusat lingkaran. Diketahui $\angle ABE + \angle ACE + \angle ADE = 96^o$. Besar $\angle AOE$ adalah . . . .
$A.\ 32^o$
$B.\ 48^o$
$C.\ 64^o$
$D.\ 84^o$
[Sudut Pusat dan Sudut Keliling]
Pembahasan:
Sudut ABE, sudut ACE, dan sudut ADE adalah sudut-sudut keliling yang sama-sama menghadap busur AE (busur yang sama). Ingat bahwa semua sudut keliling yang menghadap busur yang sama pasti memiliki besar sudut yang sama. Misalkan:
$\angle ABE = \angle ACE = \angle ADE = x$
$\angle ABE + \angle ACE + \angle ADE = 96^o$
$x + x + x = 96^o$
$3x = 96^o$
$x = 32^o$
$\angle ABE = \angle ACE = \angle ADE = 32^o$
Sudut AOE adalah sudut pusat dan bersama-sama dengan sudut keliling ABE menghadap busur AE (busur yang sama), sehingga:
$\begin{align}
\angle AOE &= 2 \times \angle ABE\\
&= 2 \times 32^o\\
&= 64^o\\
\end{align}$
jawab: C.
Soal nomor 3:
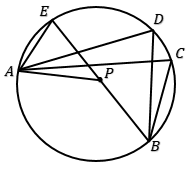
Perhatikan gambar!
Titik P adalah pusat lingkaran. Jika $\angle AEB + \angle ADB + \angle ACB = 228^o$, besar $\angle APE$ adalah . . . .
$A.\ 32^o$
$B.\ 28^o$
$C.\ 24^o$
$D.\ 20^o$
[Sudut Pusat dan Sudut Keliling]
Pembahasan:
Sudut AEB, sudut ADB, dan sudut ACB adalah tiga sudut keliling yang menghadap busur yang sama, yaitu busur AB. Perlu diingat bahwa semua sudut keliling yang menghadap busur yang sama memiliki besar sudut yang sama. Misalkan:
$\angle AEB = \angle ADB = \angle ACB = x$
$\angle AEB + \angle ADB + \angle ACB = 228^o$
$x + x + x = 228^o$
$3x = 228^o$
$x = 76^o$
$\angle AEB = \angle ADB = \angle ACB = 76^o$
Sudut APB adalah sudut pusat dan bersama-sama dengan sudut keliling AEB menghadap busur yang sama, yaitu busur AB. Dengan demikian:
$\begin{align}
\angle APB &= 2 \times \angle AEB\\
&= 2 \times 76^o\\
&= 152^o\\
\end{align}$
$\angle APB + \angle APE = 180^o$ → sudut berpelurus.
$152^o + \angle APE = 180^o$
$\begin{align}
\angle APE &= 180^o - 152^o\\
&= 28^o\\
\end{align}$
jawab: B.
Soal nomor 4:
Perhatikan gambar!
Titik O adalah titik pusat lingkaran. Garis AC adalah diameter lingkaran. Besar sudut ADB adalah . . . .
$A.\ 37^o$
$B.\ 53^o$
$C.\ 74^o$
$D.\ 106^o$
[Sudut Pusat dan Sudut Keliling]
Pembahasan:
$\angle AOB + \angle BOC = 180^o$ → sudut berpelurus.
$\angle AOB + 74^o = 180^o$
$\begin{align}
\angle AOB &= 180^o - 74^o\\
&= 106^o
\end{align}$
Sudut ADB adalah sudut keliling dan bersama-sama dengan sudut pusat AOB menghadap busur AB (busur yang sama). Sehingga:
$\begin{align}
\angle ADB &= \dfrac12 \times \angle AOB\\
&= \dfrac12 \times 106^o\\
&= 53^o\\
\end{align}$
jawab: B.
Soal nomor 5:
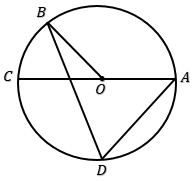
Perhatikan gambar berikut!
Titik O adalah titik pusat lingkaran. Jika besar sudut ADB $= 70^o$, maka besar sudut BOC adalah . . . .
$A.\ 30^o$
$B.\ 40^o$
$C.\ 50^o$
$D.\ 60^o$
[Sudut Pusat dan Sudut Keliling]
Pembahasan:
Sudut ADB adalah sudut keliling dan bersama-sama dengan sudut pusat AOB menghadap busur AB (busur yang sama). Sehingga:
$\begin{align}
\angle AOB &= 2 \times \angle ADB\\
&= 2 \times 70^o\\
&= 140^o
\end{align}$
$\angle AOB + \angle BOC = 180^o$ → sudut berpelurus.
$140^o + \angle BOC = 180^o$
$\begin{align}
\angle BOC &= 180^o - 140^o\\
&= 40^o\\
\end{align}$
jawab: B.
Soal nomor 6:
Perhatikan gambar di bawah!
Garis AB adalah diameter lingkaran, besar $\angle BAC = 3x^o$, dan besar $\angle ABC = 2x^o$. Nilai dari $x$ adalah . . . .
A. 24
B. 20
C. 18
D. 16
[Sudut Pusat dan Sudut Keliling]
Pembahasan:
Sudut ACB adalah sudut keliling yang menghadap diameter, sehingga besar $\angle ACB = 90^o$.
$\angle BAC + \angle ABC + \angle ACB = 180^o$ → sudut dalam segitiga.
$3x^o + 2x^o + 90^o = 180^o$
$5x^o = 180^o - 90^o$
$5x^o = 90^o$
$x = 18$
jawab: C.
Soal nomor 7:
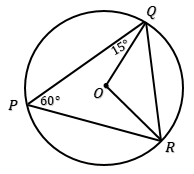
Perhatikan gambar berikut!
Besar $\angle PQO = 15^o$ dan besar $\angle QPR = 60^o$, maka besar $\angle PQR$ adalah . . . .
$A.\ 30^o$
$B.\ 45^o$
$C.\ 55^o$
$D.\ 60^o$
[Sudut Pusat dan Sudut Keliling]
Pembahasan:
Sudut QPR adalah sudut keliling dan bersama-sama dengan sudut pusat QOR menghadap busur QR, sehingga:
$\begin{align}
\angle QOR &= 2 \times \angle QPR\\
&= 2 \times 60^o\\
&= 120^o\\
\end{align}$
Segitiga QOR adalah segitiga sama kaki karena OR = OQ = jari-jari. Dengan demikian besar $\angle OQR = \angle ORQ$. Misalkan $\angle OQR = \angle ORQ = x$, maka:
$\angle QOR + \angle OQR + \angle ORQ = 180^o$ → sudut dalam segitiga.
$120^o + x + x = 180^o$
$2x = 180^o - 120^o$
$2x = 60^o$
$x = 30^o$
$\angle OQR = 30^o$
$\begin{align}
\angle PQR &= \angle PQO + \angle OQR\\
&= 15^o + 30^o\\
&= 45^o\\
\end{align}$
jawab: B.
Soal nomor 8:
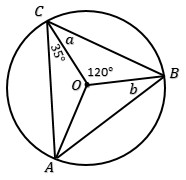
Perhatikan gambar berikut!
Nilai dari $a + b$ adalah . . . .
$A.\ 45^o$
$B.\ 50^o$
$C.\ 55^o$
$D.\ 60^o$
[Sudut Pusat dan Sudut Keliling]
Pembahasan:
Sudut BAC adalah sudut keliling dan menghadap busur yang sama dengan sudut pusat BOC, sehingga:
$\begin{align}
\angle BAC &= \dfrac12 \times \angle BOC\\
&= \dfrac12 \times 120^o\\
&= 60^o\\
\end{align}$
Segitiga AOC adalah segitiga sama kaki karena OA = OC = jari-jari, sehingga:
$\angle CAO = \angle ACO = 35^o$ → dalam segitiga sama kaki, sudut yang berhadapan sama besar.
$\angle BAC = \angle BAO + \angle CAO$
$60^o = \angle BAO + 35^o$
$60^o - 35^o = \angle BAO$
$25^o = \angle BAO$
Segitiga OAB adalah segitiga sama kaki, sehingga:
$b = \angle ABO = \angle BAO = 25^o$
Segitiga BOC adalah segitiga sama kaki, sehingga:
$\angle OCB = \angle OBC = a$
$\angle BOC + \angle OCB + \angle OBC = 180^o$ → sudut dalam segitiga.
$120^o + a + a = 180^o$
$2a = 180^o - 120^o$
$2a = 60^o$
$a = 30^o$
$a + b = 30^o + 25^o = 55^o$
jawab: C.
Demikianlah ulasan serta contoh soal dan pembahasan tentang sudut pusat dan sudut keliling, semoga bermanfaat.
www.maretong.com




Post a Comment for "Sudut Pusat dan Sudut Keliling"
Jika ada saran dan kritik yang sifatnya membangun atau ada koreksi silahkan tuliskan di kolom komentar.