Pengertian Luas Permukaan Limas
Rumus dan Cara Menghitung Luas Permukaan Limas serta Contoh Soal dan Pembahasan Super Lengkap. Luas permukaan limas adalah luas alas limas ditambah luas sisi tegak limas. Seperti yang sudah adik-adik ketahui bahwa sisi tegak limas adalah bangun datar berbentuk segitiga, seperti segitiga siku-siku, segitiga sama kaki, segitiga sama sisi, dan segitiga sembarang. Sementara alas limas bisa berbentuk segitiga atau segi empat bahkan segi banyak yang lain seperti segilima, segienam dan lain-lain. Dengan demikian untuk menghitung luas permukaan kubus dibutuhkan keteterampilan menghitung luas bangun datar segiempat dan luas bangun datar segitiga, pastikan bahwa adik-adik sudah terampil. Okelah kalau begitu, kita langsung ke contoh soal dan pembahasan. Ingat dan jangan lupa bahwa rumus luas permukaan limas adalah luas alas ditambah luas sisi tegak limas.Contoh Soal dan Pembahasan Luas Permukaan Limas
Contoh Soal nomor 1:Diketahui sebuah limas dengan alas persegi yang panjang sisinya 18 cm. Jika tinggi limas 12 cm, maka luas permukaan limas tersebut adalah . . . . $cm^2$.
A. 568
B. 684
C. 748
D. 864
[Rumus dan Cara Menghitung Luas Permukaan Limas Alas Persegi]
Pembahasan:
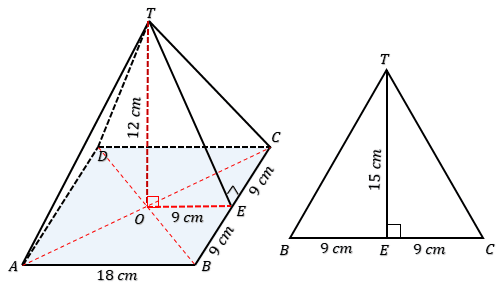
Perhatikan gambar limas di bawah!
Perhatikan segitiga EOT !
OT adalah tinggi limas = 12 cm. Panjang OE sama dengan setengah panjang AB = 9 cm. Dengan begitu panjang ET bisa dihitung dengan teorema atau tripel Pythagoras. Dengan tripel Pyth didapat panjang ET = 15 cm. Kalau masih bingung dengan tripel Pyth, baiklah kita hitung dengan teorema Pyth.
$\begin{align}
ET^2 &= OE^2 + OT^2\\
&= 9^2 + 12^2\\
&= 81 + 144\\
&= 225\\
ET &= \sqrt{225}\\
&= 15\ cm\\
\end{align}$
Panjang ET sudah didapat, sekarang kita dapat menghitung luas segitiga BCT. Perhatikan segitiga BCT !
$\begin{align}
L\Delta BCT &= \dfrac12.BC.ET\\
&= \dfrac{1}{\cancel2}.\cancelto9{18}.15\\
&= 9.15\\
&= 135\ cm^2\\
\end{align}$
Sisi tegak limas dengan alas persegi merupakan empat buah segitiga kongruen sehingga luas setiap segitiga adalah sama. Berarti luas sisi tegak limas sama dengan 4 kali luas segitiga BCT. Dengan demikian luas permukaan limas bisa dihitung.
$\begin{align}
L &= L_a + 4.L\Delta BCT\\
&= 18.18 + 4.135\\
&= 324 + 540\\
&= 864\ cm^2\\
\end{align}$
jawab: D.
Contoh Soal nomor 2:
Sebuah limas mempunyai alas persegi panjang yang panjangnya 32 cm dan lebarnya 18 cm. Jika tinggi limas 12 cm, maka luas permukaan limas tersebut adalah . . . . $cm^2$.
A. 840
B. 1.228
C. 1.416
D. 1.840
[Rumus dan Cara Menghitung Luas Permukaan Limas Alas Persegi Panjang]
Pembahasan:
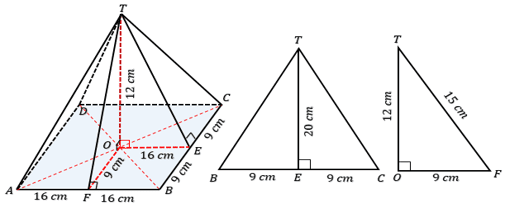
Perhatikan gambar limas persegi panjang di bawah!
Sisi tegak limas persegi panjang merupakan dua pasang segitiga kongruen. Segitiga ABT kongruen dengan segitiga CDT, sehingga luas segitiga ABT sama dengan luas segitiga CDT. Segitiga BCT kongruen dengan segitiga ADT, sehingga luas segitiga BCT sama dengan luas segitiga ADT. Dengan demikian luas sisi tegak limas adalah 2 kali luas segitiga ABT ditambah 2 kali luas segitiga BCT. Luas alas mudah dihitung karena merupakan persegi panjang. Mari kita tinjau segitiga ABT terlebih dahulu.
Perhatikan segitiga OFT !
Panjang OT sama dengan tinggi limas = 12 cm, OF sama dengan setengah BC = 9 cm. Panjang FT bisa dihitung dengan tripel pyth atau teorema Pyth. Dengan tripel Pyth didapat panjang FT = 15 cm.
Dengan rumus Pyth:
$\begin{align}
FT^2 &= OF^2 + OT^2\\
&= 9^2 + 12^2\\
&= 81 + 144\\
&= 225\\
FT &= \sqrt{225}\\
&= 15\ cm\\
\end{align}$
Setelah FT didapat, kita bisa menghitung luas segitiga ADT.
$\begin{align}
L\Delta ADT &= \dfrac12.AB.FT\\
&= \dfrac{1}{\cancel2}.\cancelto{16}{32}.15\\
&= 16.15\\
&= 240\ cm^2\\
\end{align}$
Sekarang kita tinjau segitiga BCT, perhatikan segitiga OET !
Panjang OT sama denga tinggi limas = 12 cm, OE sama dengan setengah AB = 16 cm. Dengan tripel Pyth didapat panjang ET = 20 cm.
Dengan rumus Pyth:
$\begin{align}
ET^2 &= OE^2 + OT^2\\
&= 16^2 + 12^2\\
&= 256 + 144\\
&= 400\\
ET &= \sqrt{400}\\
&= 20\ cm\\
\end{align}$
Setelah ET didapat, kita bisa menghitung luas segitiga BCT.
$\begin{align}
L\Delta BCT &= \dfrac12.BC.ET\\
&= \dfrac12.18.20\\
&= 180\ cm^2\\
\end{align}$
Luas permukaan limas:
$\begin{align}
L &= L_a + 2.L\Delta ABT + 2.L\Delta BCT\\
&= 32.18 + 2.240 + 2.180\\
&= 576 + 480 + 360\\
&= 1.416\ cm^2\\
\end{align}$
jawab: C.
Contoh Soal nomor 3:
Diketahui limas dengan alas segitiga sama sisi mempunyai luas alas $36\sqrt{3}\ cm^2$. Jika panjang rusuk tegaknya 10 cm, maka luas permukaan limas adalah . . . . $cm^2$.
$A.\ 36\sqrt{3} + 96$
$B.\ 36\sqrt{3} + 144$
$C.\ 36\sqrt{3} + 192$
$D.\ 36\sqrt{3} + 288$
[Rumus dan Cara Menghitung Luas Permukaan Limas Alas Segitiga]
Pembahasan:
Perhatikan gambar limas segitiga di bawah!
Sisi tegak limas segitiga sama sisi merupakan 3 segitiga kongruen. Segitiga ABT, segitiga BCT, dan segitiga ACT adalah kongruen sehingga luas segitiga ABT sama dengan luas segitiga BCT sama dengan luas segitiga ACT. Dengan demikian luas sisi tegak limas T.ABC sama dengan 3 kali luas segitiga ABT. Supaya luas segitiga ABT bisa didapat, kita hitung panjang AB terlebih dahulu.
Ingat rumus luas segitiga sama sisi.
$L = \dfrac14s^2\sqrt{3}$
$\begin{align}
L\Delta ABC &= \dfrac14.AB^2\sqrt{3}\\
36\cancel{\sqrt{3}} &= \dfrac14.AB^2\cancel{\sqrt{3}}\\
4.36 &= AB^2\\
AB &= \sqrt{4.36}\\
&= 2.6\\
&= 12\ cm\\
\end{align}$
Perhatikan segitiga ABT ! Dengan tripel Pyth didapat panjang PT = 8 cm.
$\begin{align}
L\Delta ABT &= \dfrac12.AB.PT\\
&= \dfrac{1}{\cancel2}.\cancelto6{12}.8\\
&= 6.8\\
&= 48\ cm^2\\
\end{align}$
Luas permukaan limas:
$L = L_a + 3.L\Delta ABT$
$= 36\sqrt{3} + 3.48$
$= (36\sqrt{3} + 144)\ cm^2$
Contoh Soal nomor 4:
Sebuah limas mempunyai alas belah ketupat dengan panjang diagonal-diagonal 12 cm dan 16 cm. Jika panjang rusuk tegak limas 13 cm, maka luas permukaan limas tersebut adalah . . . . $cm^2$.
A. 96
B. 156
C. 216
D. 336
[Rumus dan Cara Menghitung Luas Permukaan Limas Alas Belah Ketupat]
Pembahasan:
Perhatikan gambar limas belah ketupat di bawah!
Sisi tegak limas belah ketupat merupakan 4 segitiga kongruen. Segitiga ABT, segitiga BCT, segitiga CDT, dan segitiga ADT adalah segitiga-segitiga kongruen, sehingga luasnya adalah sama. Dengan demikian luas sisi tegak limas T.ABCD sama dengan 4 kali luas segitiga ABT. Diagonal-diagonal belah ketupat saling membagi dua sama panjang. Jika AC = 16, maka OA = OC = 8 cm dan BC = 12, maka OB = OD = 6 cm. Perhatikan segitiga AOB, dengan tripel Pyth didapat panjang AB = BC = CD = AD = 10 cm. Perhatikan segitiga BET ! Dengan tripel Pyth didapat ET = 12 cm.
Sekarang perhatikan segitiga ABT !
$\begin{align}
L\Delta ABT &= \dfrac12.AB.ET\\
&= \dfrac{1}{\cancel2}.10.\cancelto6{12}\\
&= 10.6\\
&= 60\ cm^2\\
\end{align}$
Luas alas limas, alas merupakan belah ketupat:
$\begin{align}
L_a &= \dfrac12.d_1.d_2\\
&= \dfrac12.16.12\\
&= 96\ cm^2\\
\end{align}$
Luas permukaan limas:
$\begin{align}
L &= L_a + 4.L\Delta ABT\\
&= 96 + 4.60\\
&= 96 + 240\\
&= 336\ cm^2\\
\end{align}$
jawab: D.
Contoh Soal nomor 5:
Diketahui sebuah limas dengan alas persegi mempunyai volume $1.280\ cm^3$. Jika panjang rusuk alas 16 cm, maka luas permukaan limas tersebut adalah . . . . $cm^2$.
A. 500
B. 600
C. 700
D. 800
[Rumus dan Cara Menghitung Luas Permukaan Limas Alas Persegi]
Pembahasan:
$\begin{align}
V &= \dfrac13L_a.t\\
1280 &= \dfrac13.16.16.t\\
t &= 1280 : \dfrac{16.16}{3}\\
&= \cancelto{80}{1280} \times \dfrac{3}{\cancel{16}.16}\\
&= \cancelto5{80} \times \dfrac{3}{\cancel{16}}\\
&= 5.3\\
&= 15\ cm\\
\end{align}$
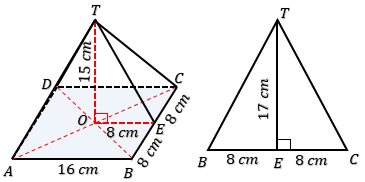
Perhatikan gambar limas persegi di bawah!
Perhatikan segitiga EOT !
OT adalah tinggi limas = 15 cm. Panjang OE sama dengan setengah panjang AB = 8 cm. Dengan begitu panjang ET bisa dihitung dengan teorema atau tripel Pythagoras. Dengan tripel Pyth didapat panjang ET = 17 cm. Kalau masih bingung dengan tripel Pyth, baiklah kita hitung dengan teorema Pyth.
$\begin{align}
ET^2 &= OE^2 + OT^2\\
&= 8^2 + 15^2\\
&= 64 + 225\\
&= 289\\
ET &= \sqrt{289}\\
&= 17\ cm\\
\end{align}$
Panjang ET sudah didapat, sekarang kita dapat menghitung luas segitiga BCT. Perhatikan segitiga BCT !
$\begin{align}
L\Delta BCT &= \dfrac12.BC.ET\\
&= \dfrac{1}{\cancel2}.\cancelto8{16}.17\\
&= 8.17\\
&= 136\ cm^2\\
\end{align}$
Sisi tegak limas dengan alas persegi merupakan empat buah segitiga kongruen sehingga luas setiap segitiga adalah sama. Berarti luas sisi tegak limas sama dengan 4 kali luas segitiga BCT. Dengan demikian luas permukaan limas bisa dihitung.
$\begin{align}
L &= L_a + 4.L\Delta BCT\\
&= 16.16 + 4.136\\
&= 256 + 544\\
&= 800\ cm^2\\
\end{align}$
jawab: D.
Contoh Soal nomor 6:
Sebuah limas dengan alas berbentuk persegi mempunyai keliling alas 64 cm dan jumlah luas sisi tegak $544\ cm^2$. Tinggi limas tersebut adalah . . . .
A. 9 cm
B. 10 cm
C. 12 cm
D. 15 cm
[Rumus dan Cara Menghitung Luas Permukaan Limas Alas Persegi]
Pembahasan:
Alas limas merupakan persegi dan keliling alas = 64 cm, berarti panjang sisi alas = 16 cm (panjang sisi persegi = keliling persegi dibagi 4). Sisi tegak limas persegi merupakan 4 buah segitiga kongruen. Jika luas sisi tegak limas $544\ cm^2$, maka luas salah satu segitiga adalah $544\ cm^2 : 4 = 136\ cm^2$.
Perhatikan gambar di bawah!
Perhatikan segitiga BCT, luas segitiga BCT $= 136\ cm^2$
$\begin{align}
L &= \dfrac12.BC.ET\\
136 &= \dfrac{1}{\cancel2}.\cancelto8{16}.ET\\
136 &= 8.ET\\
ET &= 17\ cm\\
\end{align}$
Perhatikan segitiga OET !
$\begin{align}
OT^2 &= ET^2 - OE^2\\
&= 17^2 - 8^2\\
&= 289 - 64\\
&= 225\\
OT &= \sqrt{225}\\
&= 15\ cm\\
\end{align}$
Tinggi limas = OT = 15 cm.
jawab: D.
Demikianlah pembahasan rumus dan cara menghitung luas permukaan limas serta contoh soal dan pembahasan, semoga bermanfaat.
BACA JUGA:
1. Teorema dan Tripel Pythagoras
2. Bangun Datar Segitiga
3. Bangun Datar Segiempat
www.maretong.com




Post a Comment for "Rumus Luas Permukaan Limas"
Jika ada saran dan kritik yang sifatnya membangun atau ada koreksi silahkan tuliskan di kolom komentar.