Rumus Luas Permukaan Prisma

Daftar isi

• 1 Pengertian dan Rumus Luas Permukaan Prisma
• 2 Contoh Soal dan Pembahasan Luas Permukaan Prisma

Pengertian dan Rumus Luas Permukaan Prisma

Rumus dan Cara Menghitung Luas Permukaan Prisma serta Contoh Soal dan Pembahasan Super Lengkap. Luas permukaan prisma adalah luas seluruh sisi-sisi prisma, yaitu luas alas + luas atas + luas sisi samping atau selimut atau selubung prisma. Trik untuk menghitung luas permukaan prisma pada dasarnya sama untuk semua soal yaitu dengan menghitung luas alas dan luas sisi samping. Ingat, luas alas $(L_a)$ sama dengan luas atas/atap sehingga luas atas/atap tidak perlu dicari karena luas alas + luas atas/atap sama dengan dua kali luas alas. Luas sisi samping adalah keliling alas prisma $(K_a)$ dikali dengan tinggi prisma $(t)$. Secara matematis luas permukaan prisma dirumuskan sebagai berikut:

$L = 2 \times L_a + K_a \times t$

$L →$ luas permukaan prisma
$L_a →$ luas alas atau atas prisma
$K_a →$ keliling alas prisma
$t →$ tinggi prisma

Pelajari rumus dan cara menghitung luas permukaan prisma pada contoh soal dan pembahasan yang berikut.

Contoh Soal dan Pembahasan Luas Permukaan Prisma

Contoh Soal nomor 1:
Sebuah prisma tegak mempunyai alas berbentuk persegi yang panjang sisinya 10 cm. Jika tinggi prisma 15 cm, maka luas permukaan prisma tersebut adalah . . . . $cm^2$.
A. 600
B. 700
C. 800
D. 900
[Rumus dan Cara Menghitung Luas Permukaan Prisma Persegi]

Pembahasan:
Alas prisma berbentuk persegi dengan panjang sisi 10 cm, berarti luas alas $(L_a)$ dan keliling alas $(K_a)$ prisma bisa dihirung.
$\begin{align}
L_a &= 10.10\\
&= 100\ cm^2\\
\\
K_a &= 4.10\\
&= 40\ cm\\
\\
L &= 2 \times L_a + K_a \times t\\
&= 2 \times 100 + 40 \times 15\\
&= 200 + 600\\
&= 800\ cm^2\\
\end{align}$

Contoh Soal nomor 2:
Sebuah prisma tanpa tutup memiliki alas persegi dengan panjang diagonal $8\sqrt{2}\ cm$. Jika tinggi prisma 12 cm, luas permukaan prisma tersebut adalah . . . . $cm^2$.
A. 342
B. 432
C. 448
D. 844
[Rumus dan Cara Menghitung Luas Permukaan Prisma Tanpa Tutup]

Pembahasan:
Alas prisma adalah persegi dengan panjang diagonal (PD) $8\sqrt{2}\ cm$, kita harus cari panjang sisi alas (s) prisma terlebih dahulu. Perhatikan bahwa prisma tanpa tutup.
$\begin{align}
PD &= s\sqrt{2}\\
8\cancel{\sqrt{2}} &= s\cancel{\sqrt{2}}\\
8 &= s\\
\\
L_a &= s^2\\
&= 8.8\\
&= 64\ cm^2\\
\\
K_a &= 4s\\
&= 4.8\\
&= 32\ cm\\
\\
L &= L_a + K_a \times t\\
&= 64 + 32 \times 12\\
&= 64 + 384\\
&= 448\ cm^2\\
\end{align}$
jawab: C.

Contoh Soal nomor 3:
Sebuah prisma tegak segi empat mempunyai panjang, lebar, dan tinggi dengan perbandingan 4 : 3 : 5. Jika volume prisma 1.620 $cm^3$, maka luas permukaan prisma tersebut adalah . . . . $cm^2$.
A. 486
B. 684
C. 846
D. 964
[Rumus dan Cara Menghitung Luas Permukaan Prisma Persegi Panjang]

Pembahasan:
Misalkan:
$\begin{align}
p &= 4n\\
l &= 3n\\
t &= 5n\\
\\
V &= plt\\
1620 &= 4n.3n.5n\\
1620 &= 60n^3\\
27 &= n^3\\
n &= \sqrt[3]{27}\\
n &= 3\\
\\
p &= 4.3\\
&= 12\\
l &= 3.3\\
&= 9\\
t &= 5.3\\
&= 15\\
\\
L_a &= pl\\
&= 12.9\\
&= 108\ cm^2\\
\\
K_a &= 2p + 2l\\
&= 2.12 + 2.9\\
&= 24 + 18\\
&= 42\ cm\\
\\
L &= 2 \times L_a + K_a \times t\\
&= 2 \times 108 + 42 \times 15\\
&= 216 + 630\\
&= 846\ cm^2\\
\end{align}$
jawab: C.

Contoh Soal nomor 4:
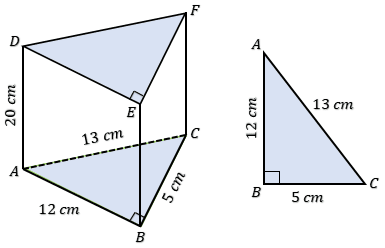
Sebuah prisma tegak mempunyai alas segitiga yang panjang sisi-sisinya 5 cm, 12 cm, dan 13 cm. Jika tinggi prisma 20 cm, maka luas prisma tersebut adalah . . . . $cm^2$.
A. 440
B. 540
C. 660
D. 780
[Rumus dan Cara Menghitung Luas Permukaan Prisma Segitiga Siku-siku]

Pembahasan:
Perhatikan gambar prisma di bawah! Alas prisma adalah segitiga siku-siku ABC. Luas alas $(L_a)$ dan keliling alas $(K_a)$ prisma bisa dihitung. Luas prisma artinya sama dengan luas permukaan prisma $(L)$.

$\begin{align}
L_a &= \dfrac12.AB.BC\\
&= \dfrac12.12.5\\
&= 30\ cm^2\\
\\
K_a &= AB + BC + AC\\
&= 12 + 5 + 13\\
&= 30\ cm\\
\\
L &= 2 \times L_a + K_a \times t\\
&= 2 \times 30 + 30 \times 20\\
&= 60 + 600\\
&= 660\ cm^2\\
\end{align}$
jawab: C.

Contoh Soal nomor 5:
Sebuah prisma mempunyai alas belah ketupat yang panjang diagonal-diagonalnya 10 cm dan 24 cm. Jika panjang rusuk tegak prisma 14 cm, luas prisma tersebut adalah . . . . $cm^2$.
A. 689
B. 896
C. 968
D. 1.224
[Rumus dan Cara Menghitung Luas Permukaan Prisma Belah Ketupat]

Pembahasan:
Perhatikan gambar prisma di bawah! Alas prisma adalah belah ketupat ABCD. Belah ketupat mempunyai empat sisi yang sama panjang dan diagonal-diagonalnya saling berpotongan tegak lurus dan saling membagi dua sama panjang. Dengan teorema atau tripel Pythagoras, panjang AB, BC, CD, dan AD didapat 13 cm.

Luas alas dan keliling alas prisma bisa dihitung.
$\begin{align}
L_a &= \dfrac12.d_1.d_2\\
&= \dfrac12.10.24\\
&= 120\ cm^2\\
\\
K_a &= 4.AB\\
&= 4.13\\
&= 52\ cm\\
\\
L &= 2 \times L_a + K_a \times t\\
&= 2 \times 120 + 52 \times 14\\
&= 240 + 728\\
&= 968\ cm^2\\
\end{align}$
jawab: C.

Contoh Soal nomor 6:
Prisma dengan alas segitiga sama sisi yang panjang sisinya 8 cm mempunyai panjang rusuk tegak $10\sqrt{3}\ cm$. Luas permukaan prisma tersebut adalah . . . . $cm^2$.
$A.\ 168\sqrt{3}$
$B.\ 272\sqrt{3}$
$C.\ 347\sqrt{3}$
$D.\ 423\ sqrt{3}$
[Rumus dan Cara Menghitung Luas Permukaan Prisma Segitiga Sama Sisi]

Pembahasan:
Perhatikan gambar di bawah! Alas prisma adalah segitiga sama sisi ABC.

$\begin{align}
CP^2 &= BC^2 - BP^2\\
&= 8^2 - 4^2\\
&= 64 - 16\\
&= 48\\
CP &= \sqrt{48}\\
&= \sqrt{16.3}\\
&= 4\sqrt{3}\ cm\\
\\
L_a &= \dfrac12.AB.CP\\
&= \dfrac12.8.4\sqrt{3}\\
&= 16\sqrt{3}\\
\\
K_a &= AB + BC + AC\\
&= 8 + 8 + 8\\
&= 24\ cm\\
\\
L &= 2 \times L_a + K_a \times t\\
&= 2 \times 16\sqrt{3} + 24 \times 10\sqrt{3}\\
&= 32\sqrt{3} + 240\sqrt{3}\\
&= 272\sqrt{3}\\
\end{align}$
jawab: B.

Contoh Soal nomor 7:
Alas sebuah prisma tanpa tutup berbentuk segitiga siku-siku yang luasnya $60\ cm^2$ dan salah satu sisi penyikunya 15 cm. Jika tinggi prisma 22 cm, maka luas prisma tersebut adalah . . . . $cm^2$.
A. 680
B. 720
C. 860
D. 940
[Rumus dan Cara Menghitung Luas Permukaan Prisma Tanpa Tutup]

Pembahasan:
Perhatikan gambar prisma dengan alas segitiga ABC di bawah!

Alas prisma adalah segitiga ABC, panjang sisi-sisi yang lain dapat dihitung dengan rumus luas segitiga.
$\begin{align}
Luas\ \Delta ABC &= \dfrac12.AB.BC\\
60 &= \dfrac12.15.BC\\
BC &= 60 : \dfrac{15}{2}\\
&= \cancelto4{60} \times \dfrac{2}{\cancel{15}}\\
&= 4 \times 2\\
&= 8\ cm\\
\end{align}$
Dengan teorema atau tripel Pyth didapat panjang AC = 17 cm. Dengan begitu keliling alas dan luas prisma bisa dihitung, jangan lupa bahwa prismanya tanpa tutup.
$\begin{align}
K_a &= AB + BC + AC\\
&= 15 + 8 + 17\\
&= 40\ cm\\
\\
L &= L_a + K_a \times t\\
&= 60 + 40 \times 22\\
&= 60 + 880\\
&= 940\ cm^2\\
\end{align}$
jawab: D.

Contoh Soal nomor 8:
Sebuah prisma mempunyai alas berbentuk jajargenjang dengan panjang sisi-sisi sejajar 12 cm dan 10 cm. Jika tinggi jajar genjang 8 cm dan panjang rusuk tegak trapesium 15 cm, maka luas permukaan prisma adalah . . . . $cm^2$.
A. 482
B. 684
C. 750
D. 852
[Rumus dan Cara Menghitung Luas Permukaan Prisma Jajargenjang]

Pembahasan:
Perhatikan gambar prisma di bawah!

Alas prisma adalah jajargenjang ABCD.
$\begin{align}
L_a &= AB.DP\\
&= 12.8\\
&= 96\ cm^2\\
\\
K_a &= AB + BC + CD + AD\\
&= 12 + 10 + 12 + 10\\
&= 44\ cm\\
\\
L &= 2 \times L_a + K_a \times t\\
&= 2 \times 96 + 44 \times 15\\
&= 192 + 660\\
&= 852\ cm^2\\
\end{align}$
jawab: D.

Contoh Soal nomor 9:
Perhatikan gambar prisma di bawah!

Panjang EF = 8 cm, AB = 16 cm, BF = 17 cm, dan BC = 9 cm. Luas permukaan prisma adalah . . . . $cm^2$.
A. 864
B. 900
C. 1.100
D. 1.200
[Rumus dan Cara Menghitung Luas Permukaan Prisma Trapesium Siku-siku]

Pembahasan:
Luas permukaan prisma adalah luas trapesium ABFE + luas trapesium CDHG + luas persegi panjang ABCD + luas persegi panjang ADHE + luas persegi panjang BCGF + luas persegi panjang EFGH. Luas trapesium ABFE = luas trapesium CDHG.

Luas trapesium ABFE $(L_1)$:
AP = EF = 8 cm.
AB = AP + BP
16 = 8 + BP → BP = 8 cm
Perhatikan segitiga BFP !
Dengan tripel Pyth didapat FP = 15 cm
AE = FP = 15 cm
$\begin{align}
L_1 &= \dfrac12(EF + AB).AE\\
&= \dfrac12(8 + 16).15\\
&= \dfrac12.24.15\\
&= 180\ cm^2\\
\end{align}$

Luas trapesium CDHG $(L_2)$:
$L_2 = L_1 = 180\ cm^2$

Luas persegi panjang ABCD $(L_3)$:
$\begin{align}
L_3 &= AB.BC\\
&= 16.9\\
&= 144\ cm^2\\
\end{align}$

Luas persegi panjang ADHE $(L_4)$:
$\begin{align}
L_4 &= AD.AE\\
&= 9.15\\
&= 135\ cm^2\\
\end{align}$

Luas persegi panjang BCGF $(L_5)$:
$\begin{align}
L_5 &= BC.BF\\
&= 9.17\\
&= 153\ cm^2\\
\end{align}$

Luas persegi panjang EFGH $(L_6)$:
$\begin{align}
L_6 &= EF.FG\\
&= 8.9\\
&= 72\ cm^2\\
\end{align}$

Luas permukaan prisma $(L)$:
$\begin{align}
L &= L_1 + L_2 + L_3 + L_5 + L_6\\
&= 180 + 180 + 144 + 135 + 153 + 72\\
&= 864\ cm^2\\
\end{align}$
jawab: A.

Contoh Soal nomor 10:
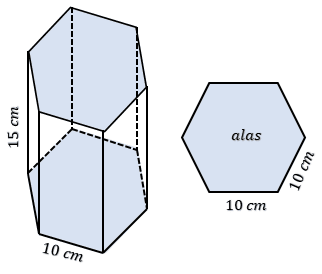
Sebuah prisma mempunyai alas berbentuk segienam beraturan yang panjang sisinya 10 cm. Jika tinggi prisma 15 cm maka luas permukaan prisma tersebut adalah . . . .
$A.\ 200(3 + \sqrt{3})\ cm^2$
$B.\ 300(3 + \sqrt{3})\ cm^2$
$C.\ 400(3 + \sqrt{3})\ cm^2$
$D.\ 500(3 + \sqrt{3})\ cm^2$
[Rumus dan Cara Menghitung Luas Permukaan Prisma Segienam]

Pembahasan:
Perhatikan gambar prisma di bawah!

Alas prisma merupakan segienam beraturan:
$\begin{align}
L_a &= \dfrac32s^2\sqrt{3}\\
&= \dfrac32.10^2\sqrt{3}\\
&= 150\sqrt{3}\ cm\\
\\
K_a &= 6s\\
&= 6.10\\
&= 60\ cm\\
\\
L &= 2 \times L_a + K_a \times t\\
&= 2 \times 150\sqrt{3} + 60 \times 15\\
&= 300\sqrt{3} + 900\\
&= 300(3 + \sqrt{3})\ cm^2\\
\end{align}$
jawab: B.

Contoh Soal nomor 11:
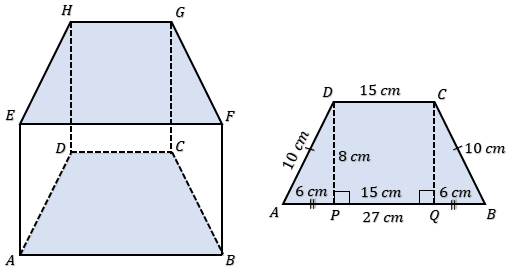
Diketahui alas sebuah prisma berbentuk trapesium sama kaki dengan panjang garis sejajar 15 cm dan 27 cm serta panjang kaki trapesium 10 cm. Jika tinggi prisma 32 cm, maka luas prisma adalah . . . . $cm^2$.
A. 2.152
B. 2.160
C. 2.320
D. 2.656
[Rumus dan Cara Menghitung Luas Permukaan Prisma Trapesium Sama Kaki]

Pembahasan:
Perhatikan gambar trapesium di bawah!

Alas prisma adalah trapesium sama kaki ABCD. Panjang CD = PQ = 15 cm. Misalkan panjang $AP = BQ = x.$
$AB = AP + PQ + BQ$
$27 = x + 15 + x$
$27 = 2x + 15$
$27 - 15 = 2x$
$12 = 2x$
$x = 6$
$AP = BQ = x = 6$

Perhatikan segitiga APD !
Dengan tripel Pyth didapat panjang DP = 8 cm. Dengan begitu luas dan keliling alas prisma bisa dihitung.
$\begin{align}
L_a &= \dfrac12(AB + CD).DP\\
&= \dfrac12(27 + 15).8\\
&= \dfrac12.42.8\\
&= 168\ cm^2\\
\\
K_a &= AB + BC + CD + AD\\
&= 27 + 10 + 15 + 10\\
&= 62\ cm\\
\\
L &= 2 \times L_a + K_a \times t\\
&= 2 \times 168 + 62 \times 32\\
&= 336 + 1984\\
&= 2320\ cm^2\\
\end{align}$
jawab: C.

Contoh Soal nomor 12:
Sebuah prisma dengan alas berbentuk belah ketupat yang kelilingnya 68 cm dan panjang salah satu diagonalnya 16 cm. Jika volume prisma 4.320 $cm^3$ maka luas permukaan prisma adalah . . . . $cm^3$.
A. 1.704
B. 2.074
C. 3.407
D. 4.701
[Rumus dan Cara Menghitung Luas Permukaan Prisma Belah Ketupat]

Pembahasan:
Perhatikan gambar di bawah!

Alas prisma adalah belah ketupat ABCD. Belah ketupat memiliki 4 sisi yang sama panjang. Jika keliling belah ketupat 68 cm, maka panjang sisi belah ketupat = 17 cm. Perhatikan segitiga AOB, dengan tripel Pyth, didapat panjang OA = 15 cm. Dengan demikian panjang kedua diagonal belah ketupat adalah 16 cm dan 30 cm.
$\begin{align}
L_a &= \dfrac12.d_1.d_2\\
&= \dfrac12.16.30\\
&= 240\ cm^2\\
\\
V &= L_a.t\\
4320 &= 240.t\\
t &= 18\ cm\\
\\
L &= 2 \times L_a + K_a \times t\\
&= 2 \times 240 + 68 \times 18\\
&= 480 + 1224\\
&= 1.704\ cm^2\\
\end{align}$
jawab: A.

Demikianlah pembahasan tentang rumus dan cara menghitung luas permukaan prisma, semoga bermanfaat.

BACA JUGA:
1. Teorema dan Tripel Pythagoras
2. Bangun Datar Segitiga
3. Bangun Datar Segiempat

SHARE THIS POST

www.maretong.com

Share :