Daftar isi
Pengertian Panjang Kerangka Kubus dan Balok
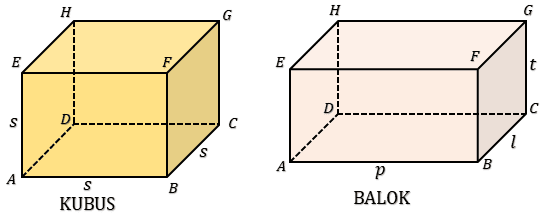
Rumus dan Cara Menghitung Panjang Kerangka Kubus dan Balok serta Contoh Soal dan Pembahasan Super Lengkap. Panjang kerangka kubus atau balok adalah panjang seluruh rusuk kubus atau balok. Perhatikan gambar di bawah!Rumus Panjang Kerangka Kubus (PKK):
$PKK = 12s$
$s$ → Panjang rusuk kubus
Rumus Panjang Kerangka Balok (PKB):
$PKB = 4(p + l + t)$
Pelajari rumus dan cara menghitung panjang kerangka kubus dan balok serta contoh soal dan pembahasan berikut.
Contoh Soal dan Pembahasan Panjang Kerangka Kubus dan Balok
Contoh Soal nomor 1:Panjang kawat yang dibutuhkan untuk membuat satu kerangka kubus dengan panjang rusuk 8 cm adalah . . . .
A. 112 cm
B. 96 cm
C. 84 cm
D. 76 cm
[Rumus Panjang Kerangka Kubus dan Balok]
Pembahasan:
Panjang Kerangka Kubus (PKK):
$\begin{align}
PKK &= 12s\\
&= 12.8\\
&= 96\ cm\\
\end{align}$
jawab: B.
Contoh Soal nomor 2:
Andi ingin membuat 5 kerangka kubus yang panjang rusuknya 25 cm, panjang kawat yang dibutuhkan oleh Andi adalah . . . .
A. 12 meter
B. 13 meter
C. 14 meter
D. 15 meter
[Rumus Panjang Kerangka Kubus dan Balok]
Pembahasan:
Panjang kawat (PK) sama dengan banyak kerangka kubus $(n)$ dikali panjang kerangka kubus (PKK).
$\begin{align}
PK &= n.PKK\\
&= n.12s\\
&= 5.12.25\\
&= 1500\ cm\\
&= 15\ meter\\
\end{align}$
jawab: D.
Contoh Soal nomor 3:
Sebuah kawat yang panjangnya 3,5 meter digunakan untuk membuat kerangka kubus yang panjang rusuknya 28 cm. Panjang kawat yang tidak terpakai adalah . . . .
A. 12 cm
B. 14 cm
C. 15 cm
D. 17 cm
[Rumus Panjang Kerangka Kubus dan Balok]
Pembahasan:
Panjang kawat (PK) = 3,5 meter = 350 cm. Kawat yang tidak terpakai atau sisa kawat sama dengan panjang kawat (PK) dikurangi panjang kerangka kubus (PKK).
$\begin{align}
PKK &= 12s\\
&= 12.28\\
&= 336\ cm\\
\\
Sisa\ kawat &= PK - PKK\\
&= 350 - 336\\
&= 14\ cm\\
\end{align}$
jawab: B.
Contoh Soal nomor 4:
Sebuah kawat sepanjang 8 meter digunakan untuk membuat kerangka kubus yang panjang rusuknya 16 cm. Banyak kerangka kubus yang dapat dibuat dan sisa kawat adalah . . . .
A. 4 buah sisi 16 cm
B. 4 buah sisa 32 cm
C. 5 buah sisa 18 cm
D. 5 buah sisa 32 cm
[Rumus Panjang Kerangka Kubus dan Balok]
Pembahasan:
Panjang kawat (PK) = 8 meter = 800 cm. Panjang kawat (PK) sama dengan banyak kerangka kubus $(n)$ dikali panjang kerangka kubus (PKK).
$\begin{align}
PK &= n.PKK\\
PK &= n.12s\\
800 &= n.12.16\\
800 &= n.192\\
n &= \dfrac{800}{192}\\
&= 4\dfrac{\boxed{32}}{192}\\
\end{align}$
Banyak kerangka kubus yang dapat dibuat adalah 4 dan sisa kawat adalah 32 cm (lihat angka yang di dalam kotak).
Contoh Soal nomor 5:
Winsar akan membuat 5 buah kerangka kubus dari batang-batang kawat yang panjangnya 1 meter. Jika panjang rusuk kubus 25 cm maka banyak batang kawat yang diperlukan adalah . . . .
A. 10 batang
B. 12 batang
C. 15 batang
D. 18 batang
[Rumus Panjang Kerangka Kubus dan Balok]
Pembahasan:
Panjang batang-batang kawat = 1 meter = 100 cm. Panjang kawat (PK) sama dengan banyak kerangka kubus $(n)$ dikali panjang kerangka kubus (PKK).
$\begin{align}
PK &= n.PKK\\
&= n.12s\\
&= 5.12.25\\
&= 1500\ cm\\
\end{align}$
Karena panjang kawat (PK) = 1500 cm dan panjang batang-batang kawat = 100 cm, maka banyaknya batang-batang kawat yang dibutuhkan adalah 15 batang.
jawab: C.
Contoh Soal nomor 6:
Sebuah kawat yang panjangnya 4,8 meter akan dibuat menjadi kerangka kubus yang panjang rusuknya $7\dfrac23$ cm, maka panjang kawat yang tidak terpakai adalah . . . .
A. 15 cm
B. 18 cm
C. 20 cm
D. 24 cm
[Rumus Panjang Kerangka Kubus dan Balok]
Pembahasan:
Panjang kawat (PK) = 4,8 meter = 480 cm. Panjang rusuk kubun $= 7\dfrac23\ cm = \dfrac{23}{3}\ cm$. Panjang kawat (PK) sama dengan banyak kerangka kubus $(n)$ dikali panjang kerangka kubus (PKK).
$\begin{align}
PK &= n.PKK\\
PK &= n.12s\\
480 &= n.\cancelto4{12}.\dfrac{23}{\cancel3}\\
480 &= n.4.23\\
480 &= n.92\\
n &= \dfrac{480}{92}\\
&= 5\dfrac{\boxed{20}}{92}\\
\end{align}$
Panjang kawat yang tidak terpakai adalah 20 cm (lihat angka yang di dalam kotak).
jawab: C.
Contoh Soal nomor 7:
Panjang kawat yang diperlukan untuk membuat kerangka balok berukuran $20\ cm \times 16\ cm \times 12\ cm$ adalah . . . .
A. 176 cm
B. 184 cm
C. 192 cm
D. 216 cm
[Rumus Panjang Kerangka Kubus dan Balok]
Pembahasan:
Panjang Kerangka Balok (PKB):
$\begin{align}
PKB &= 4(p + l + t)\\
&= 4(20 + 16 + 12)\\
&= 4(48)\\
&= 192\ cm\\
\end{align}$
jawab: C.
Contoh Soal nomor 8:
Kawat sepanjang 12 meter akan dibuat kerangka balok yang berukuran panjang 27 cm, lebar 21 cm, dan tinggi 12 cm. Paling banyak kerangka balok yang dapat dibuat adalah . . . .
A. 4 buah
B. 5 buah
C. 6 buah
D. 8 buah
[Rumus Panjang Kerangka Kubus dan Balok]
Pembahasan:
Panjang kawat (PK) harus sama dengan banyak kerangka balok $(n)$ dikali panjang kerangka balok (PKB).
Panjang Kerangka Balok (PKB):
$\begin{align}
PKB &= 4(p + l + t)\\
&= 4(27 + 21 + 12)\\
&= 4(60)\\
&= 240\ cm\\
\\
PK &= n.PKB\\
1200 &= n.240\\
n &= \dfrac{1200}{240}\\
&= 5\ buah.
\end{align}$
Dalam hal ini tidak ada kawat yang sisa atau lebih.
jawab: B.
Contoh Soal nomor 9:
Sebuah kerangka balok yang dengan ukuran panjang 20 cm, lebar 12 cm, dan tinggi t cm. Jika panjang kawat kerangka balok 1,6 meter maka tinggi balok adalah . . . .
A. 8 cm
B. 9 cm
C. 10 cm
D. 12 cm
[Rumus Panjang Kerangka Kubus dan Balok]
Pembahasan:
Panjang Kerangka Balok (PKB) = 1,6 meter = 160 cm.
$\begin{align}
PKB &= 4(p + l + t)\\
\cancelto{40}{160} &= \cancelto14(20 + 12 + t)\\
40 &= 20 + 12 + t\\
40 &= 32 + t\\
40 - 32 &= t\\
8 &= t\\
\end{align}$
jawab: A.
Contoh Soal nomor 10:
Perbandingan panjang, lebar, dan tinggi sebuah balok adalah 5 : 3 : 2. Jika panjang kerangka balok 200 cm, maka panjang kerangka balok tersebut adalah . . . .
A. 25 cm
B. 20 cm
C. 18 cm
D. 15 cm
[Rumus Panjang Kerangka Kubus dan Balok]
Pembahasan:
Panjang kerangka balok (PKB) = 200 cm.
Misalkan:
$\begin{align}
p &= 5n\\
l &= 3n\\
t &= 2n\\
\\
PKB &= 4(p + l + t)\\
\cancelto{50}{200} &= \cancelto14(5n + 3n + 2n)\\
50 &= 10n\\
n &= 5\\
\\
p &= 5n\\
&= 5.5\\
&= 25\ cm\\
\end{align}$
Contoh Soal nomor 11:
Sebatang kawat dapat membuat 6 buah kerangka balok dengan ukuran panjang 20 cm, lebar 15 cm, dan tinggi 10 cm. Dengan kawat yang sama, banyak kerangka kubus dengan panjang rusuk 18 cm yang dapat dibuat adalah . . . .
A. 5 buah
B. 6 buah
C. 7 buah
D. 8 buah
[Rumus Panjang Kerangka Kubus dan Balok]
Pembahasan:
Panjang kawat (PK) sama dengan 6 dikali panjang kerangka balok (PKB). Karena kawat yang sama digunakan untuk membuat kerangka kubus, maka panjang kawat (PK) harus sama dengan banyak kerangka kubus $(n)$ dikali panjang kerangka kubus (PKK).
$\begin{align}
PK &= 6.PKB\\
&= 6.4(p + l + t)\\
&= 6.4(20 + 15 + 10)\\
&= 6.4.45 \ \cdots\ *\\
\\
PK &= n.PKK\\
&= n.12s\\
&= n.12.18\ \cdots\ **\\
\\
6.4.45 &= n.12.18\\
n &= \dfrac{\cancel6.\cancel4.45}{\cancelto3{18}.\cancelto3{12}}\\
&= \dfrac{45}{9}\\
&= 5\\
\end{align}$
jawab: A.
Contoh Soal nomor 12:
Seorang pedagang ikan hias ingin membuat kerangka akuarium dengan menggunakan alumunium. Kerangka tersebut berbentuk balok dengan ukuran $2\ m \times 1\ m \times 50\ cm$. Jika harga alumunium Rp30.000,00 per meter, maka biaya yang diperlukan untuk membuat kerangka akuarium tersebut adalah . . . .
A. Rp600.000,00
B. Rp450.000,00
C. Rp420.000,00
D. Rp105.000,00
[Rumus Panjang Kerangka Kubus dan Balok]
Pembahasan:
Panjang kerangka akuarium (PKA):
$\begin{align}
PKA &= 4(p + l + t)\\
&= 4(2 + 1 + 0,5)\\
&= 4(3,5)\\
&= 14\ meter\\
\\
Biaya &= 14 \times 30.000\\
&= 420.000\\
\end{align}$
jawab: C.
Demikianlah ulasan tentang rumus dan cara menghitung panjang kerangka kubus dan balok serta contoh soal dan pembahasan, semoga bermanfaat.
www.maretong.com

Post a Comment for "Rumus Panjang Kerangka Kubus dan Balok"
Jika ada saran dan kritik yang sifatnya membangun atau ada koreksi silahkan tuliskan di kolom komentar.