Pengertian dan Rumus Vulume Prisma
Rumus dan Cara Menghitung Volume Prisma Tegak Segitiga dan Segiempat serta Contoh Soal dan Pembahasan Super Lengkap. Menghitung volume prisma sebenarnya sangat sederhana, karena cukup menghitung luas alas kemudian kalikan dengan tinggi prisma. Sederhana sekali bukan? Hanya saja prisma memiliki bentuk alas yang sangat beraneka ragam seperti segitiga siku-siku, segitiga sama kaki, segitiga sama sisi, persegi, persegi panjang, belah ketupat, dan lain-lain. Untuk itu adik-adik diharapkan sudah menguasai bangun datar segitiga, bangun datar segiempat, dan Teorema dan Tripel Pythagoras. Lihat linknya di bawah postingan!Volume Prisma:
$V = L_a \times t$
$V → volume\ prisma$
$L_a → luas\ alas\ prisma$
$t → tinggi\ prisma$
Supaya lebih paham tentang rumus dan cara menghitung volume prisma, silahkan pelajari contoh soal dan pembahasan berikut.
Contoh Soal dan Pembahasan Volume Prisma
Contoh Soal nomor 1:Sebuah prisma mempunyai alas persegi dengan panjang sisi alas 8 cm. Jika tinggi prisma 12 cm, maka volume prisma tersebut adalah . . . . $cm^3$
A. 876
B. 867
C. 768
D. 687
[Rumus dan cara menghitung volume prisma]
Pembahasan:
Perhatikan gambar prisma dengan alas persegi di bawah!
Alas prisma adalah persegi ABCD. Tinggi prisma adalah AE.
$\begin{align}
L_a &= 8.8\\
&= 64\ cm^2\\
\\
V &= L_a \times t\\
&= 64.12\\
&= 768\ cm^3\\
\end{align}$
Contoh Soal nomor 2:
Sebuah prisma tegak segiempat mempunyai panjang, lebar, dan tinggi dengan perbandingan 4 : 3 : 5. Jika luas alas prisma tersebut 300 $cm^2$, maka volume prisma tersebut adalah . . . . $cm^3$
A. 9.000
B. 8.400
C. 7.500
D. 6.800
[Rumus dan cara menghitung volume prisma]
Pembahasan:
Misalkan:
$\begin{align}
p &= 4n\\
l &= 3n\\
t &= 5n\\
\\
L_a &= p.l\\
300 &= 4n.3n\\
300 &= 12n^2\\
n^2 &= 25\\
n &= 5\\
\\
p &= 4.5\\
&= 20\ cm\\
l &= 3.5\\
&= 15\ cm\\
t &= 5.5\\
&= 25\ cm\\
\\
V &= L_a \times t\\
&= 300 \times 25\\
&=7.500\ cm^3\\
\end{align}$
jawab: C.
Contoh Soal nomor 3:
Sebuah prisma tegak segiempat dengan alas berbentuk persegi. Jika luas permukaan prisma tersebut 680 $cm^2$ dan tinggi prisma 12 cm, maka volume prisma tersebut adalah . . . . $cm^3$
A. 800
B. 1.200
C. 1.450
D. 1.600
[Rumus dan cara menghitung volume prisma]
Pembahasan:
Luas Permukaan Prisma (L) adalah dua kali luas alas $(L_a)$ + keliling alas dikali tinggi $(t)$. Sedangkan luas alas adalah panjang sisi alas $(s)$ dikali panjang sisi alas $(s)$ dan keliling alas adalah empat kali panjang sisi alas $(s)$.
$\begin{align}
L &= 2 \times L_a + K_a \times t\\
680 &= 2 \times s \times s + 4s \times 12\\
680 &= 2s^2 + 48s\\
0 &= 2s^2 + 48s - 680\\
0 &= s^2 + 24s - 340\\
0 &= (s - 10)(s + 34)\\
s &= 10\ cm\\
s &= -34 → tidak\ memenuhi\\
\\
V &= L_a \times t\\
&= s^2 \times t\\
&= 10^2 \times 12\\
&= 100 \times 12\\
&= 1.200\ cm^3\\
\end{align}$
jawab: B.
Contoh Soal nomor 4:
Sebuah prisma tegak segitiga mempunyai alas dengan panjang sisi-sisi 5 cm, 12 cm, dan 13 cm. Jika tinggi prisma 20 cm maka volume prisma tersebut adalah . . . . $cm^3$.
A. 300
B. 400
C. 500
D. 600
[Rumus dan cara menghitung volume prisma]
Pembahasan:
Alas berbentuk segitiga dan berdasarkan ukuran sisi-sisinya kita tahu bahwa alasnya adalah segitiga siku-siku. Perhatikan gambar di bawah!
$\begin{align}
L_a &= \dfrac12.12.5\\
&= 30\\
\\
V &= L_a \times t\\
&= 30 \times 20\\
&= 600\ cm^3\\
\end{align}$
jawab: D.
Contoh Soal nomor 5:
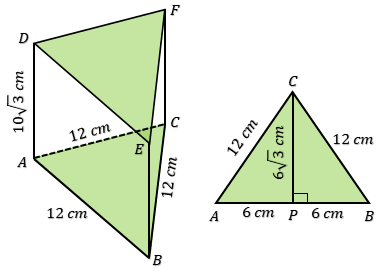
Sebuah prisma tegak segitiga mempunyai alas segitiga sama sisi dengan panjang sisi 12 cm. Jika panjang rusuk tegak prisma $10\sqrt{3}$ cm, dan ke dalam prisma dimasukkan gula pasir yang beratnya 1,25 kg/liter, maka berat gula pasir yang dapat ditampung oleh prisma tersebut adalah . . . .
A. 1,25 kg
B. 1,35 kg
C. 1,52 kg
D. 1,65 kg
[Rumus dan cara menghitung volume prisma]
Pembahasan:
Perhatikan gambar prisma di bawah!
Perhatikan segitiga sama sisi ABC !
$\begin{align}
CP^2 &= BC^2 - BP^2\\
&= 12^2 - 6^2\\
&= 144 - 36\\
&= 108\\
CP &= \sqrt{108}\\
&= \sqrt{36.3}\\
&= 6\sqrt{3}\\
\\
L_a &= \dfrac12.AB.CP\\
&= \dfrac12.12.6\sqrt{3}\\
&= 36\sqrt{3}\\
\\
V &= L_a \times t\\
&= 36\sqrt{3} \times 10\sqrt{3}\\
&= 36.10.3\\
&= 1080\ cm^3\\
&= \dfrac{1080}{1000}\ liter\\
&= 1,08\ liter\\
\\
Berat &= 1,08\ \cancel{liter} \times 1,25\ \dfrac{kg}{\cancel{liter}}\\
&= 1,35\ kg\\
\end{align}$
jawab: B.
Contoh Soal nomor 6:
Sebuah prisma tegak mempunyai alas belah ketupat dengan panjang diagonal-diagonalnya 16 cm dan 20 cm. Jika tinggi prisma 25 cm, maka volume prisma tersebut adalah . . . . $cm^3$.
A. 3.500
B. 4.000
C. 5.600
D. 7.200
[Rumus dan cara menghitung volume prisma]
Pembahasan:
$\begin{align}
L_a &= \dfrac12.d_1.d_2\\
&= \dfrac12.16.20\\
&= 160\ cm^2\\
\\
V &= L_a \times t\\
&= 160 \times 25\\
&= 4.000\ cm^3\\
\end{align}$
jawab: B.
Contoh Soal nomor 7:
Sebuah prisma tegak alasnya berbentuk belah ketupat dengan panjang diagonal 12 cm dan 16 cm. Jika luas seluruh permukaan prisma 392 $cm^2$, volume prisma adalah . . . . $cm^3$.
A. 392
B. 480
C. 584
D. 960
[Rumus dan cara menghitung volume prisma]
Pembahasan:
Perhatikan gambar di bawah!
Perhatikan segitiga AOB ! Dengan tripel Pythagoras didapat AB = 10 cm, sehingga keliling alas $K_a$ prisma dapat dihitung.
$\begin{align}
K_a &= 4.10\\
&= 40\ cm\\
\\
L_a &= \dfrac12.d_1.d_2\\
&= \dfrac12.12.16\\
&= 96\ cm^2\\
\end{align}$
Luas Permukaan Prisma (L):
$\begin{align}
L &= 2 \times L_a + K_a \times t\\
392 &= 2 \times 96 + 40 \times t\\
392 &= 192 + 40t\\
40t &= 392 - 192\\
40t &= 200\\
t &= 5\ cm\\
\\
V &= L_a \times t\\
&= 96 \times 5\\
&= 480\ cm^3\\
\end{align}$
jawab: B.
Contoh Soal nomor 8:
Panjang diagonal alas sebuah prisma yang berbentuk layang-layang adalah 12 cm dan 30 cm. Jika tinggi prisma 25 cm, volume prisma adalah . . . . $cm^3$.
A. 1.500
B. 2.250
C. 4.500
D. 9.000
[Rumus dan cara menghitung volume prisma]
Pembahasan:
$\begin{align}
L_a &= \dfrac12.d_1.d_2\\
&= \dfrac12.12.30\\
&= 180\ cm^2\\
\\
V &= L_a \times t\\
&= 180 \times 25\\
&= 4.500\ cm^3\\
\end{align}$
jawab: C.
Contoh Soal nomor 9:
Perhatikan gambar prisma berikut!
Jika panjang EF = 8 cm, AB = 16 cm, BF = 17 cm, dan BC = 9 cm. Volume prisma adalah . . . . $cm^3$.
A. 864
B. 1.240
C. 1.460
D. 1.620
[Rumus dan cara menghitung volume prisma]
Pembahasan:
Prisma pada gambar di atas adalah prisma dengan alas trapesium siku-siku ABFE. Untuk menghitung volume, kita harus hitung luas trapesium ABFE terlebih dahulu. Tinggi prisma (t) adalah AD = BC = 9 cm. Perhatikan gambar trapesium ABFE di bawah!
Dengan teorema atau tripel Pythagoras didapat FP = 15 cm. AE = FP = 15 cm.
Luas trapesium ABFE (alas):
$\begin{align}
L_a &= \dfrac12(AB + EF) \times AE\\
&= \dfrac12(16 + 8) \times 15\\
&= \dfrac12 \times 24 \times 15\\
&= 180\ cm^2\\
\\
V &= L_a \times t\\
&= 180 \times 9\\
&= 1.620\ cm^3\\
\end{align}$
jawab: D.
Contoh Soal nomor 10:
Diketahui prisma tegak dengan tinggi 17 cm dan alasnya berbentuk jajargenjang. Jika alas jajargenjang 12 cm dan tinggi 9 cm, volume prisma adalah . . . . $cm^3$.
A. 612
B. 918
C. 1.836
D. 2.754
[Rumus dan cara menghitung volume prisma]
Pembahasan:
Perhatikan gambar prisma di bawah!
Alas prisma adalah jajargenjang ABCD. Dengan begitu kita bisa menghitung luas alas prisma.
$\begin{align}
L_a &= AB.DP\\
&= 12.9\\
&= 108\ cm^2\\
\\
V &= L_a \times t\\
&= 108 \times 17\\
&= 1.836\ cm^3\\
\end{align}$
jawab: C.
Contoh Soal nomor 11:
Sebuah prisma dengan alas berbentuk belah ketupat yang kelilingnya 52 cm dan panjang salah satu diagonalnya 10 cm. Jika luas selubung prisma 1.040 $cm^2$, maka volume prisma tersebut adalah . . . . $cm^3$.
A. 4.800
B. 3.600
C. 2.400
D. 1.040
[Rumus dan cara menghitung volume prisma]
Pembahasan:
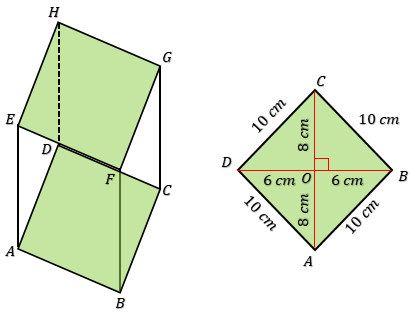
Perhatikan gambar prisma di bawah!
Belah ketupat memiliki empat sisi yang sama panjang. Karena keliling diketahui 52 cm, maka panjang sisi-sisi belah ketupat adalah 13 cm (lihat gambar). Salah satu diagonal misalkan BD = 10 cm, sehingga OB = 5 cm. Lihat segitiga AOB, dengan teorema atau tripel Pythagoras didapat panjang OA = 12 cm. Berarti AC atau diagonal yang lain sama dengan 24 cm. Karena panjang diagonal-diagonal sudah didapat, maka luas alas prisma bisa dicari.
Luas Selubung Prisma (LSP):
$\begin{align}
LSP &= K_a \times t\\
1040 &= 52 \times t\\
t &= 20\ cm\\
\\
L_a &= \dfrac12.d_1.d_2\\
&= \dfrac12.10.24\\
&= 120\ cm^2\\
\\
V &= L_a \times t\\
&= 120 \times 20\\
&= 2.400\ cm^3\\
\end{align}$
jawab: C.
Contoh Soal nomor 12:
Sebuah prisma tegak mempunyai alas segienam beraturan yang panjang sisinya 12 cm. Jika tinggi prisma 16 cm, maka volume prisma tersebut adalah . . . .
$A.\ 3.456\sqrt{3}\ cm^3$
$B.\ 4.356\sqrt{3}\ cm^3$
$C.\ 5.346\sqrt{3}\ cm^3$
$D.\ 6.345\sqrt{3}\ cm^3$
[Rumus dan cara menghitung volume prisma]
Pembahasan:
Luas alas prisma (segienam beraturan):
$\begin{align}
L_a &= \dfrac32s^2\sqrt{3}\\
&= \dfrac32.12^2\sqrt{3}\\
&= \dfrac32.144\sqrt{3}\\
&= 216\sqrt{3}\ cm^2\\
\\
V &= L_a \times t\\
&= 216\sqrt{3} \times 16\\
&= 3.456\sqrt{3}\ cm^3\\
\end{align}$
jawab: A.
Demikianlah pembahasan tentang rumus dan cara menghitung volume prisma serta contoh soal dan pembahasan, semoga bermanfaat.
BACA JUGA:
1. Teorema dan Tripel Pythagoras
2. Bangun Datar Segitiga
3. Bangun Datar Segiempat
www.maretong.com







Post a Comment for "Rumus Volume Prisma"
Jika ada saran dan kritik yang sifatnya membangun atau ada koreksi silahkan tuliskan di kolom komentar.